Lineares inhomogenes DGL Anfangswertproblem lösen?

Question

Wie löse ich dieses Anfangswertproblem?Ich erhalte komplexe Eigenwerte und komme nicht weiter. Danke!

Gegeben sei das inhomogene lineare Differenzialgleichungssystem \( \frac{d y}{d t}=A y+f \), wobei
\(A=\left(\begin{array}{cc} 2 & 1 \\ -1 & 2 \end{array}\right) \quad \text { und } \quad f(t)=\left(\begin{array}{c}\cos (t) \\-\sin (t)\end{array}\right)\)
Berechnen Sie diejenige Lösung \( y_{p} \) dieses Systems, die der Anfangsbedingung \( y_{p}(0)= \) \( (0,0)^{\top} \) genügt.

Answer 1

Hallo,

Aber was mache ich genau beim Koeffizientenvergleich

z.B. bei cos(t): ich vergleiche die Koeffizienten vor dem cos(t) der linken mit der rechten Seite.

analog für sin(t)

und wie bilde ich yp‘ ?

Du bildest jeweils die 1. Ableitung

---------->

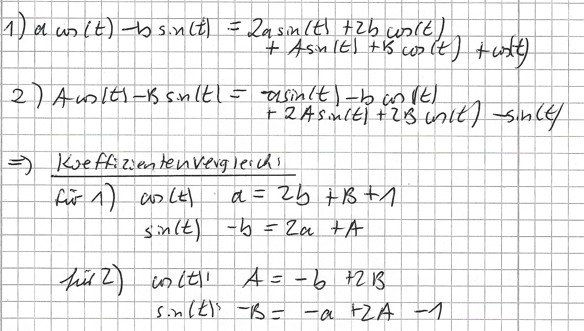
a=B=0

A= 1/2

b= -1/2

 ---->

yp1= -1/2   * cos(t)

yp2=  1/2   *sin(t)

Ich habe erhalten (ohne AWB):

\( y_{1}=C_{2} e^{2 t} \sin (t)+C_{1} e^{2 t} \cos (t)-\frac{\cos (t)}{2} \)

\( y_{2}=-C_{1} e^{2 t} \sin (t)+\frac{\sin (t)}{2}+C_{2} e^{2 t} \cos (t) \)

mit AWB:

C₁=1/2 ; C₂=0

\( y_{1}=\frac{1}{2} e^{2 t} \cos (t)-\frac{\cos (t)}{2} \)

\( y_{2}=-\frac{1}{2} e^{2 t} \sin (t)+\frac{\sin (t)}{2} \)

Comments

Vielen Dank erstmal! Aber was mache ich genau beim Koeffizientenvergleich und wie bilde ich yp‘ ? Könntest du das ausführen?