wir haben in etwa folgende Situation:
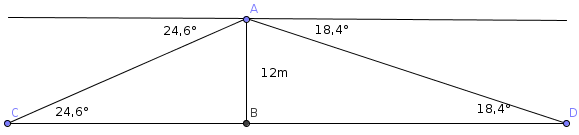
Gegeben sind die Tiefenwinkel α = 24,6° (links) und β = 18,4° (rechts) sowie die Gegenkathete (Höhe des Theodoliten = 12m).
Gesucht ist jeweils die Ankathete.
Eselsbrücke:
sin cos tan cot
G A G A
H H A G
tan(24,6°) = Gegenkathete/Ankathete, also Ankathete = Gegenkathete/tan(24,6°) ≈ 12/0,457835746 ≈ 26,21
Der nähere Messpunkt (C) liegt also ca. 26,21m von B entfernt.
tan(18,4°) = Gegenkathete/Ankathete, also Ankathete = Gegenkathete/tan(18,4°) ≈ 12/0,3326557243 ≈ 36,07
Der weiter entfernte Messpunkt (D) liegt also ca. 36,07m von B entfernt.
Damit haben die beiden Messpunkte einen Abstand voneinander von ca. 26,21m + 36,07m = 62,28m
Besten Gruß