Aufgabe:
Beweise, dass sich die Determinante einer nxn Matrix M durch Entwicklung nach einer Zeile bestimmen lässt
Problem/Ansatz:
Hallo Leute, ich gehe in der Aufgabe von drei Eigenschaften aus, die die Determinantenfunktion definiert:
1. Linearität
2. Rang(M)<n → Det(M)=0
3. Det(I)=1 mit I=Einheitsmatrix
Das ist die zugrundeliegende Formel:
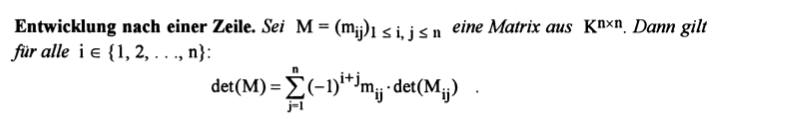
Nun geht es im Beweis darum zu zeigen, dass die 3 genannten Kriterien erfüllt sind. Im Beweis wird die Formel nur für i=1 bewiesen, wobei i für die Zeile steht, um die es geht. Mir geht es jetzt um den Beweis des 2. Punktes. Der Beweis baut darauf auf, dass die Zeilen und Spalten von M linear abhängig sind, wenn der Rang von M < n. Jetzt kommt der entscheidende Punkt: Der Beweis geht damit weiter, dass wir oBdA annehmen können, dass M zwei gleiche Spalten hat. Aber linear abhängig bedeutet doch nicht zwei gleiche Spalten. Wieso darf man bei einem derartigen Beweis so vorgehen?