WIe bestimme ich Schnittwinkel zweier Geraden im Kreis in Abhängigkeit von Innenwinkeln des Dreiecks?

Question

Im abgebildeten Dreieck ABC sind Ma und Mb Seitenmittelpunkte. Das Dreieck wurde dabei so gewählt, dass der Halbkreis über [AB]die anderen Seiten zwischen Ma und C sowie zwischen Mb und C in den Punkten A* bzw. B* schneidet.

Bestimme in diesem Dreieck den Schnittwinkel der Geraden MbA* und MaB* in Abhängigkeit von den Innenwinkeln des Dreiecks ABC.

Hat irgendjemand einen Tipp für mich, wie ich an die Lösung kommen könnte, einen Ansatz oder so etwas... Bin ratlos... Geometrie ist echt meine Schwäche...Habe es schon mit Pythagoras probiert... komme aber nicht weiter und hat mir auch nichts geholfen...

Comments

(MbMa) ist parallel zu AB. Ob du mit dieser Hilfslinie weiterkommst als zu dem beiden Winkeln ALPHA und BETA darüber, weiss ich momentan nicht.

Die Innenwinkel der Dreiecks sind übrigens ALPHA, BETA und GAMMA.

---

das hilft mir leider gerade gar nicht,

---

Was ist das doch für ein Zufall dass die Frage exakt die 2. Aufgabe der 2. Runde des Landeswettbewerbs Mathematik Baden-Würtemberg ist!!!  Ich finde es unfair anderen gegenüber, die sich selber eigene Gedanken gemacht haben, sich die Aufgabe einfach von jemandem in diesem Forum lösen zu lassen, und nicht einmal in die Frage zu schreiben, wofür die Lösung eigentlich gebraucht wird! Und jemand, der so etwas macht, hat in der ersten Runde einen 1. oder 2. Preis erhalten!!!

Diese Seite scheint irgendwie für solche Leute gemacht - Das ist schon die zweite Aufgabe dieses Wettbewerbs, die hier gestellt wird! (--> https://www.mathelounge.de/75671/teilbarkeit-gerader-zahlen-moglich-kinder-sitzen-einem-tisch )

---

Hatten wir schon oft die Dikussion, siehe FAQ: https://www.mathelounge.de/faq#qu34

Answer 1

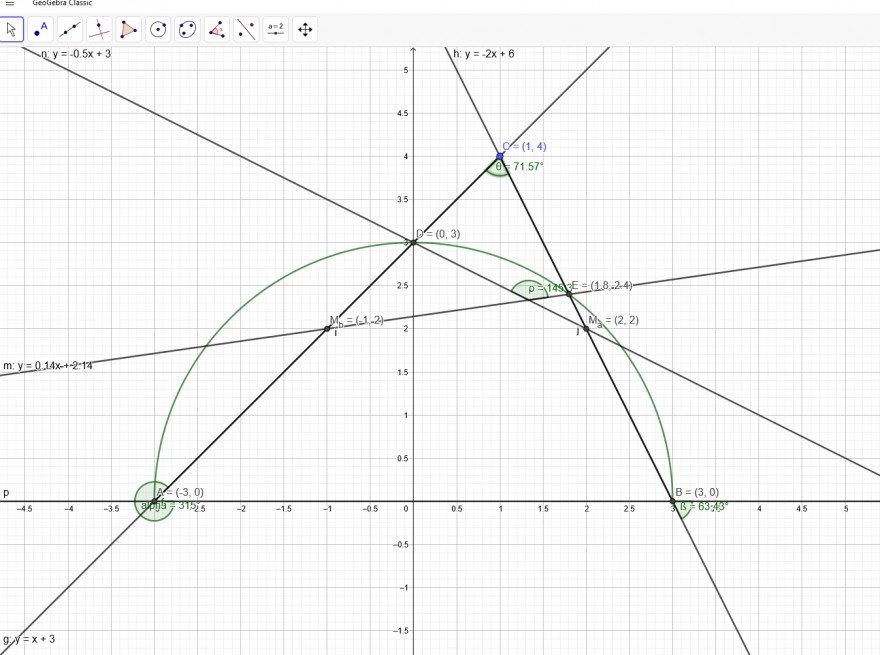
A(-3|0), B(3|0) und C(1|4)  Innenwinkel α=45°;β=63,43° und γ=71,57°

Halbkreis:

y=\( \sqrt{9-x^2} \)

Gerade durch A und C

\(\frac{y-4}{x-1} \)=\(\frac{0-4}{-3-1} \)->y=x+3

\( \sqrt{9-x^2} \)=x+3

x_1=-3->y_1=0

x_2=0->y_2=3-> D(0|3)

Gerade durch B und C->y=-2x+6->E(1,8|2,4)

Gerade durch M_b und E-> y=0,14x+2,14->m_1=0,14

Gerade durch M_a und D-> y=-0,5x+3->m_2=-0,5

tan φ=|\( \frac{m_2-m_1}{1+m_1*m_2} \)|

tan φ=|\( \frac{-0,5-0,14}{1+0,14*(-0,5)} \)|=\( \frac{64}{93} \)

φ=tan^-1(\( \frac{64}{93} \) )

φ=34,53°

Um eine Abhängigkeit zu den Innenwinkeln zu bestimmen, müsste der Punkt C variiert werden.

mfG

Text erkannt:

1

Moliets

Comments

Hallo Moliets,

Um eine Abhängigkeit zu den Innenwinkeln zu bestimmen, müsste der Punkt C variiert werden.

das wird doch 'ne ziemliche Rechnerei, wenn es überhaupt zu einem Ergebnis führt.

Die Gerade \(m_a\) durch \(M_c\) und \(M_b\) ist Mittelparallele im \(\triangle ABC\) und somit parallel zu \(b\). Die Strecke \(AA^*\) ist die Höhe \(h_a\) (schwarz gestrichelt) in \(\triangle ABC\). Daraus kann man auf die Symmetrie von \(A\) zu \(A^*\) bezüglich \(m_a\) schließen. Folglich ist \(\angle M_cM_bA^* = \gamma\) (gelb).

Das macht man auf der anderen Seite genauso und aus der Betrachtung der Parallelen zu \(M_bA^*\) und \(M_aB^*\) in \(C\) (rot gestrichelt) oder der Winkelsumme im Viereck \(M_bM_cM_aS\) folgt dann der gesuchte Winkel \(\varphi\) (violett)$$\varphi = 3 \gamma - 180°$$

---

Eine gute Idee, werde ich mir mal genau anschauen!

mfG

Moliets