Ganzrationale Funktion bestimmen Basketball Freiwurf

Question

Aufgabe:

Ein Baskettballspieler beschreibt bei einem Freiwurf näherungsweise eine Wurfparabel.

A) bestimmen sie eine ganzrationale Funktion f zweiten Grades, deren Graph den Verlauf der Wurfparabel näherungsweise beschreibt.

Info: m=-1 in Q

Problem/Ansatz:

Ansatz P(0/2) Abwurfpunkt Q(4/3) Korb

f(x)=ax‘2+Bx +c

F‘(x)=2ax+b

Text erkannt:

1

Answer 1

Wegen P(0/2) Abwurfpunkt ist der Ansatz:

f(x)=ax²+bx+2. f '(x)=2ax+b

Wegen 45° im Punkt (4|3)  gilt f '(4)=-1also (1) -1=8a+b

und wegen Q(4/3) Korb gilt                         (2) 3=16a+4b+2.

Das System aus (1) uns (2) hat die Lösungen a= - 5/16 und b=3/2.

Flugkurve; f(x)=- 5/16·x²+3/2·x+2

Comments

Vielen Dank! Ich hatte den Ansatz genau gleich nur habe ich drei Bedingungen zuerst gebildet und die c=2 also den y-Achsenabschnitt nicht direkt eingesetzt.

Answer 2

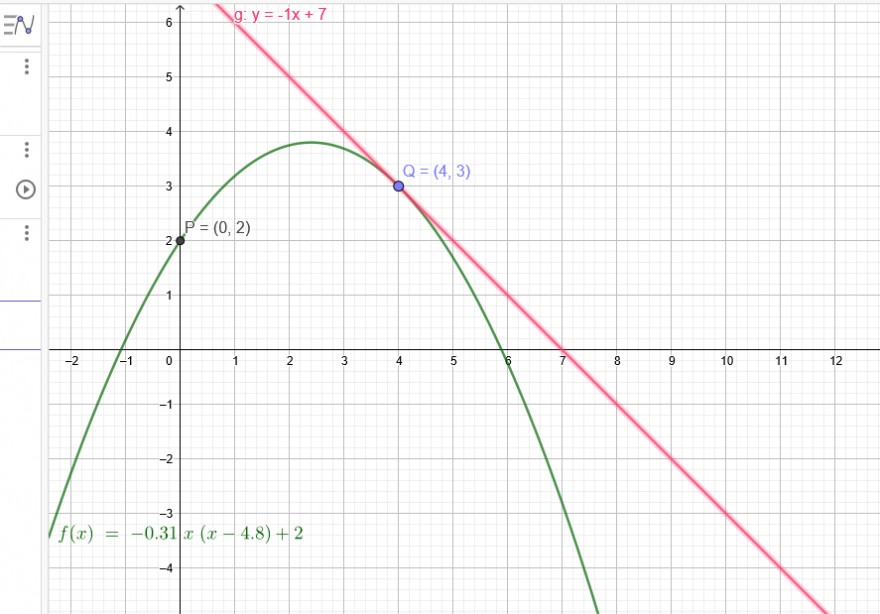
So geht es auch:

P(0|2) Abwurfpunkt Q(4|3) Korb   m=-1 in Q

Ich verschiebe um 2 Einheiten ↓ :  P(0|2)→  P´(0|0)    und   Q(4|3) →  Q´(4|1) Weiter mit der Nullstellenform der quadratischen Parabel:

Allgemein: f(x)=a•(x-N_1)•(x-N_2)

Für diese Aufgabe:  f(x)=a • x•(x-N_2)

Q´(4|1)

f(x)=a•4•(4-N_2)

1.)  a•4•(4-N_2) =1  → a•(16- 4 N_2) =1   → a=\( \frac{1}{16-4N_2} \)

f´(x)=a • [(x-N_2)+x•1]

f´(4)=a • [(4-N_2)+4]

2.) a • [8-N_2] = - 1  →  a= \( \frac{1}{N_2-8} \)

\( \frac{1}{16-4N_2} \)=\( \frac{1}{N_2-8} \)

N_2-8=16-4N_2

N_2=4,8

a= \( \frac{1}{4,8-8} \)= - 0,3125

f(x)= - 0,3125 • x•(x-4,8)

Nun wieder 2 Einheiten ↑
p(x)=- 0,3125 • x•(x-4,8)+2