Aussagen über reelle Zahlenfolgen

Question

Die folgenden Aussagen sind auf Richtigkeit zu überprüfen:

(a) Sind die Teilfolgen 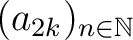und 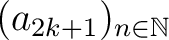beide monoton wachsend, so ist auch 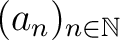monoton wachsend.

(b) Jede monotone Folge hat höchstens einen Häufungspunkt.

(c) Ist die Folge 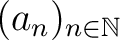streng monoton wachsend, dann ist die Folge  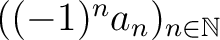 divergent.

Eine ganz kurze Erklärung pro Aussage wäre sehr wünschenswert!

LG

Answer 1

a)Gegenbeispiel: (a_2n)_n∈ℕ=2, 4, 6, 8, ...  (a_2n+1)_n∈ℕ=0, 1, 2, 3, ...

Answer 2

b) ist wahr. Die Annahme der Existenz von zwei verschiedenen Häufungspunkten lässt sich widerlegen, indem man um beide angenommenen Häufungspunkte jeweils so kleine epsilon-Umgebungen legt, dass zwischen diesen Umgebungen noch eine Lücke bleibt.

zu c) betrachte die Folge (-1, -1/2, -1/3, -1/4, ....)