Gleichschenkliges Dreieck Formeln herleiten?

Question

Aufgabe:

Ein gleichschenkliges Dreieck ist durch die Basislänge g und eine Schenkellänge s gegeben.

Leite eine Formel für die Höhe h und den Flächeninhalt A her.

Answer 1

Hallo drobbl,

 

bei einem gleichschenkligen Dreieck sind 2 Seiten - die Schenkel - gleich, die dritte Seite - die Grundseite - hat eine andere Länge.

 

Die folgende Skizze zeigt ein beliebiges gleichschenkliges Dreieck:

 

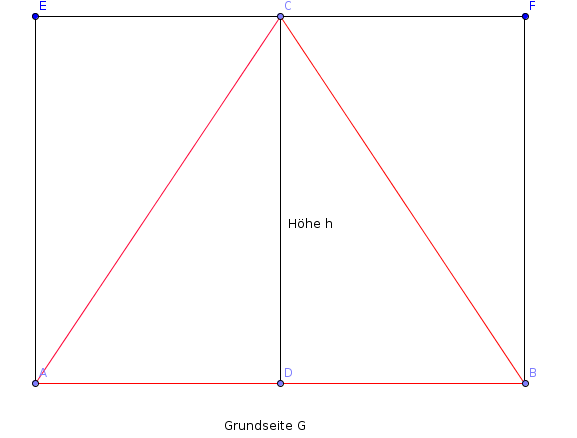
Da das Dreieck ACE die gleiche Fläche hat wie das Dreieck ADC und

DBC die gleiche Fläche wie das Dreieck BFC, sehen wir, dass für die Fläche A die Formel gilt:

A = Grundseite * Höhe / 2 = G * h / 2

 

Für die Höhe h können wir, weil wir rechts und links jeweils ein rechtwinkliges Dreieck haben, sagen:

h² + (Grundseite G / 2)² = s² (s ist einer der Schenkel), also

h² = s² - (G/2)²

h = √[s² - (G/2)²]

 

Besten Gruß

Answer 2

Hi,

Ne Skizze dazu:

für den Flächeninhalt sieht man sofort:

A = c/2*h

 

Für h gehe über Pythagoras:

h^2 + (c/2)^2 = a^2   |-(c/2)^2

h^2 = a^2 - c^2/4

h = √(a^2-c^2/4)

 

Grüße

Answer 3

Also die Formel für die Berechnung des Flächeninhalts eines Dreiecks ist Höhe (der Seite) * Seite * 1/2

Da beim Eintragen der Höhe immer rechte Winkel entstehen kann man den Satz der Pythagoras ²nehmen

also a² + b² = c² hier : Umstellung da man eine Kathete und nicht die Hypotenuse braucht.

hier ist h gesucht also (a² oder b²) also a² = c² - b² also c = s und b = g/2 und a = h also gilt

h² = s² - (g/2)² und da wir h suchen Wurzel aus beidem (Äquivalenzumformung)

h = Wurzel aus (s² -(g/2)²)