Gleichschenkliges dreieck schenkel berechnen

Question

Ein gleichschenkliges Dreieck hat einen Basis von 5,5 cm Länge und einen Flächeninhalt von 24,75 cm^2. Bestimme die Länge der Schenkel und die Größe der Innenwinkel.

Comments

\(A=\frac14\sqrt{4a^2b^2-(a^2+b^2-c^2)}\). Mit \(a=b\) folgt \(a=\frac1{2c}\sqrt{c^4+16A^2}\).

---

Nach Heron gilt:

$$A=\frac14\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}$$ 

---

Stimmt. Habe ein Quadrat am Ende der Klammer vergessen. Vielleicht könnte das jemand einfügen.

---

Ist nicht so wichtig, denke ich. Das unten drunter stimmt ja.

Answer 1

Teile das gleichschenklige Dreieck mit der Höhe "hc" in zwei rechtwinklige Dreiecke: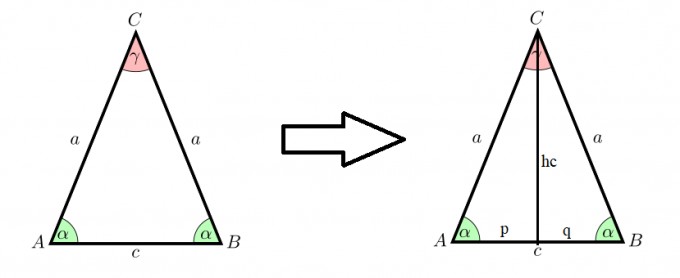

Nun musst du den Flächeninhalt auch in zwei Teilen, um die Flächeninhalt der beiden neuen rechtwinkligen Dreieck zu haben. Da es sich um ein gleichschenkliges Dreieck handelt sich die Strecken "p" und "q" beide gleichlang. Nämlich so:

p,q=5.5/2

p,q=2.75cm

Flächeninhalt im gesamten Dreieck ist wie folgt:

h_c=(2*A)/c

h_c=(2*24.75)/5.5

h_c=9cm

Wir können jetzt den Satz des Pythagoras anwenden um einen Schenkel zu bestimmen:

a=√(9^2+2.75^2)

a≈9.411cm

Die Innenwinkel können wir auch leicht bestimmen:

Kosinussatz nach Alpha umstellen, beachte (a=b)

α,β=arccos((b^2+c^2-a^2)/(2*b*c))

α,β=arccos((9.411^2+5.5^2-9.411^2)/(2*9.411*5.5))

α,β=73.01°

Beachte auch, dass α=β

γ=180°-2*73.01=33.98°