
Text erkannt:
Aufgabe 1) Bestimme den Mittelwert (Nntendurchschnitt der Klasse)
\begin{tabular}{|l|l|}
\hline Gruppe 1 & Klasse \( 10 \mathrm{a} \) \\
\hline Gruppe 2 & Klasse \( 10 \mathrm{~b} \) \\
\hline Gruppe 3 & Klasse \( 10 \mathrm{C} \) \\
\hline Gruppe 4 & Klasse \( 10 \mathrm{~d} \) \\
\hline
\end{tabular}

Text erkannt:
Setze die entsprechenden Werte für deine Versuche dann dein Ergebnis im Sarhrisammanhn und berechne
1.) \( \sum \limits_{i=1}^{6}\left(\left(x_{i}-E(X)\right) \cdot P\left(X=x_{i}\right)\right) \)
\( =\left(x_{1}-E(X)\right) \cdot P\left(X=x_{1}\right)+\left(x_{2}-E(X)\right) \cdot P\left(X=x_{2}\right)+\cdots+\left(x_{1}-F(X)\right) \cdot P\left(X=\gamma_{0}\right) \)
$$ \begin{array}{l} =(1-3,5) \cdot \frac{1}{30}+(2-3,5) \cdot \frac{1}{15}+(3-3,5) \cdot \frac{2}{5}+(a-3,5) \cdot \frac{2}{5}+(5-3,5) . \\ \frac{1}{15}+(6-3,5) \cdot \frac{1}{30}=3 \cdot E-15 \end{array} $$
2.) \( \sum \limits_{i=1}^{6}\left(\left|x_{i}-E(X)\right| \cdot P\left(X=x_{i}\right)\right) \)
$$ =|x-F(X)| \cdot P\left(X=x_{1}\right)+\left|x_{2}-E(X)\right| \cdot P\left(X=x_{2}\right)+\cdots+\left|x_{6}-E(X)\right| \cdot P(X=x $$
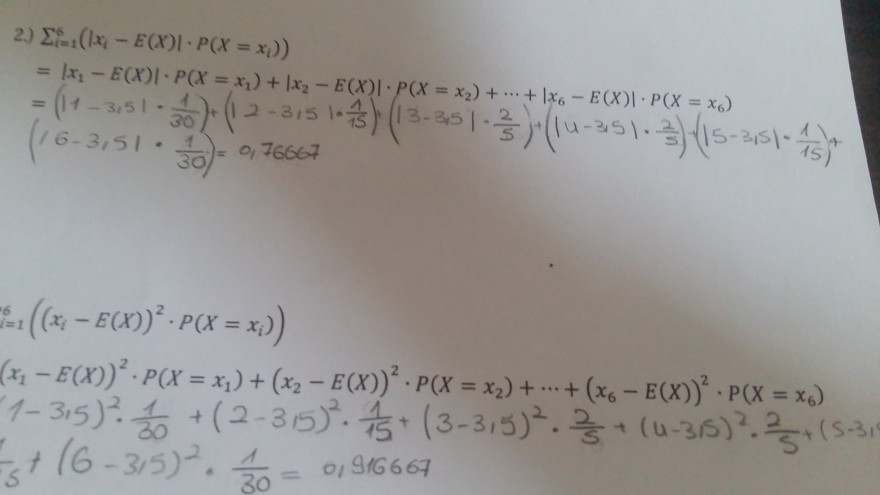
Text erkannt:
2) \( \sum \limits_{i=1}^{6}\left(\left|x_{i}-E(X)\right| \cdot P\left(X=x_{i}\right)\right) \)
\( { }_{i=1}^{6}\left(\left(x_{i}-E(X)\right)^{2} \cdot P\left(X=x_{i}\right)\right) \)
\( \left(x_{1}-E(X)\right)^{2} \cdot P\left(X=x_{1}\right)+\left(x_{2}-E(X)\right)^{2} \cdot P\left(X=x_{2}\right)+\cdots+\left(x_{6}-E(X)\right)^{2} \cdot \mathrm{P}\left(\mathrm{X}=x_{6}\right) \)
\( (1-3,5)^{2} \cdot \frac{1}{30}+(2-3,5)^{2} \cdot \frac{1}{15}+(3-3,5)^{2} \cdot \frac{2}{5}+(u-315)^{2} \cdot \frac{2}{5}+(5-31 \)
\( \frac{1}{5}+(6-3,5)^{2} \cdot \frac{1}{30}=0,916667 \)
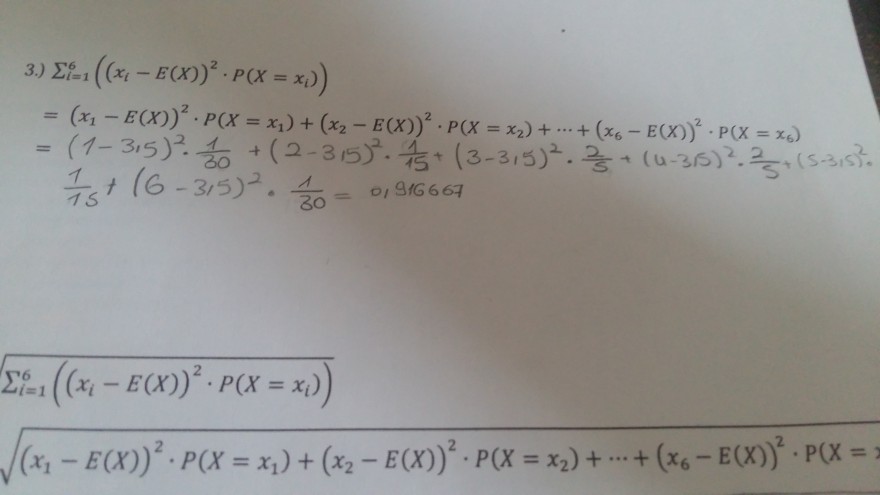
Text erkannt:
3.) \( \sum \limits_{i=1}^{6}\left(\left(x_{i}-E(X)\right)^{2} \cdot P\left(X=x_{i}\right)\right) \)
\( =\left(x_{1}-E(X)\right)^{2} \cdot P\left(X=x_{1}\right)+\left(x_{2}-E(X)\right)^{2} \cdot P\left(X=x_{2}\right)+\cdots+\left(x_{6}-E(X)\right)^{2} \cdot P\left(X=x_{6}\right) \)
\( =(1-3,5)^{2} \cdot \frac{1}{30}+(2-315)^{2} \cdot \frac{1}{15}+(3-3,5)^{2} \cdot \frac{2}{5}+(4-3 / 5)^{2} \cdot \frac{2}{5}+(5-3,15) \)
\( \frac{1}{15}+(6-3,5)^{2} \cdot \frac{1}{30}=0,916667 \)
\( \sum \limits_{i=1}^{6}\left(\left(x_{i}-E(X)\right)^{2} \cdot P\left(X=x_{i}\right)\right) \)
\( \sqrt{\left(x_{1}-E(X)\right)^{2} \cdot P\left(X=x_{1}\right)+\left(x_{2}-E(X)\right)^{2} \cdot P\left(X=x_{2}\right)+\cdots+\left(x_{6}-E(X)\right)^{2} \cdot P(X)=} \)

Text erkannt:
4.) \( \sqrt{\sum \limits_{i=1}^{6}\left(\left(x_{i}-E(X)\right)^{2} \cdot P\left(X=x_{i}\right)\right)} \)
\( =\sqrt{\left(x_{1}-E(X)\right)^{2} \cdot P\left(X=x_{1}\right)+\left(x_{2}-E(X)\right)^{2} \cdot P\left(X=x_{2}\right)+\cdots+\left(x_{4}-E(X)\right)^{2} \cdot P\left(X=\gamma_{1}\right)} \)
\( =\sqrt{(1-3,5)^{2} \cdot \frac{1}{30}+(2-35)^{2} \cdot \frac{1}{15}+(3-3 i 5)^{2} \cdot \frac{2}{5}+(4-315)^{2} \cdot \frac{2}{5}+(5-3,5)^{2} \cdot \frac{1}{15}+(6-3,5)^{2} \cdot \frac{1}{3 n}} \)
\( =0,957427 \approx 0,55 \)
\( \Rightarrow \) Die Standardabweichung beschreibt die enwartete A bweichung des Zulall variablen von ihrem Erwartung owest \( \Rightarrow \)
Problem: Ich versuche nochmal:
Wie kann man die Ergebnisse im Sachzusammenhang erläutern?
Ich habe die Erwartungswert für Klasse 10c berechnet:3,5
Und dann habe die Standardabweichung dafür berechnet. Wie kann ich es aber erläuter