Geben sie zwei Funktionsterme an, dessen zugehöriger Graph Asymptoten mit den angegebenen Gleichungen besitzt.
a) y=0
Die Funktion muss sich der x-Achse annähern, darf sie aber nicht schneiden ( Da hätte sie dann eine Nullstelle)
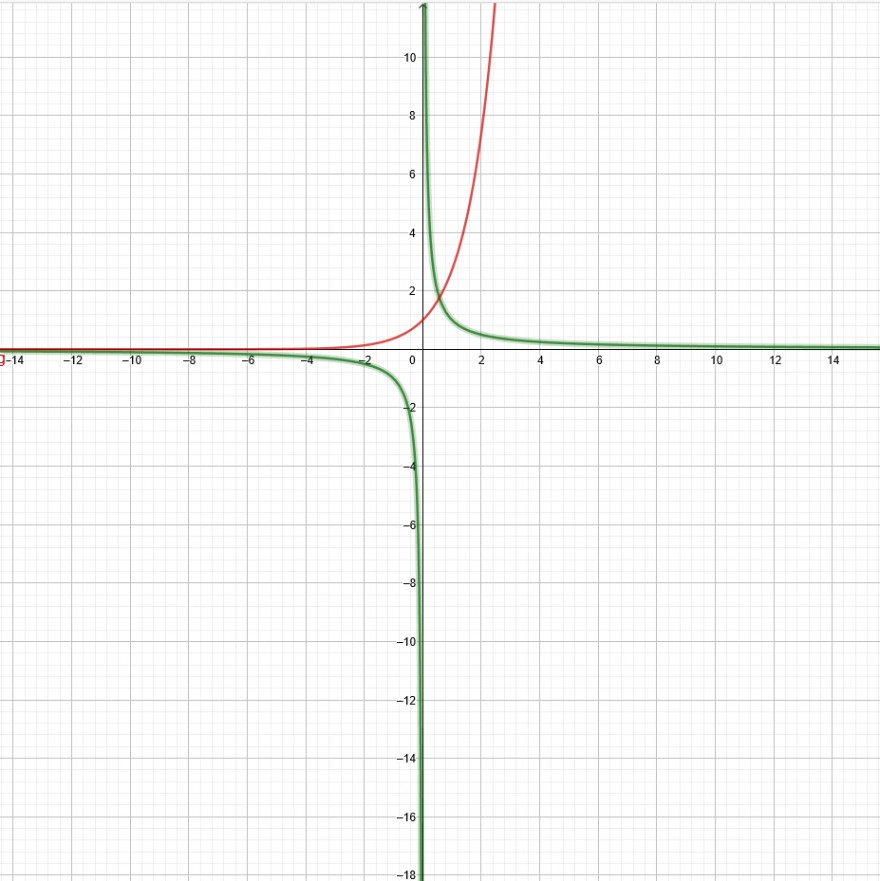
in grün: 1.) y = \( \frac{1}{x} \) → P1(4|0,25) → P2(10|0,1) auch P1(-4|-0,25) → P2(-10|-0,1) die y-Werte werden immer kleiner:
\( \lim\limits_{x\to\infty} \) \( \frac{1}{x} \)→0 Auch gegen - unendlich →0
in rot: 2.) f(x) =\( e^{x} \)
f(-10) = \( e^{-10} \) ≈ 0,00004 Hier siehst du, dass die y-Werte immer kleiner werden. Aber niemals 0 werden:
\( e^{x} \) = 0 → x* ln e= ln 0 → x* 1= ln 0 ist nicht definiert .Somit e^x niemals 0 werden Die negative x-Achse ist hier Asymptote.
Text erkannt:
\( x \)