\( \alpha=110^{\circ} ; s=65 \mathrm{~cm}=6,5\mathrm{~dm} \)
a) Berechne den Umfang der daraus gefertigten Schultüte an der Öffnung.
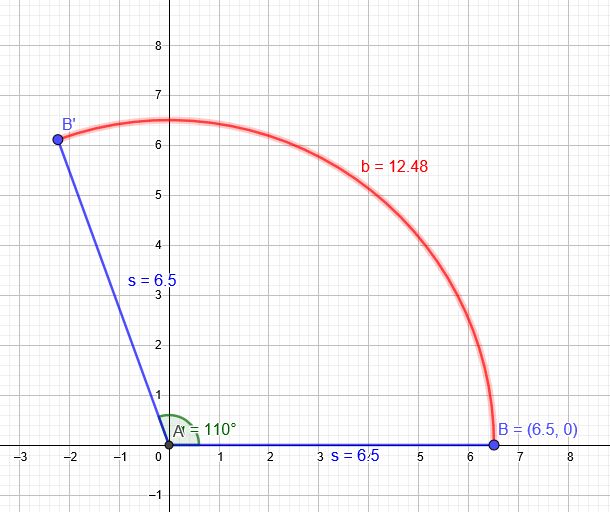
\(b= \frac{α}{360°}\cdot U \)
Allgemein: \(U =2\cdot r \cdot π \)
\(b= \frac{α}{360°}\cdot 2\cdot r \cdot π \)
\(b= \frac{110°}{360°}\cdot 2\cdot 6,5\mathrm{~dm} \cdot π\\= \frac{11}{36}\cdot 13\mathrm{~dm} \cdot π ≈12,479\mathrm{~dm}\)
b) Welche Maße hat ein kleinstmögliches Rechteck aus dem der Karton für die Schultüte geschnitten werden kann? \( \alpha=110^{\circ} ; s=65 \mathrm{~cm} \)
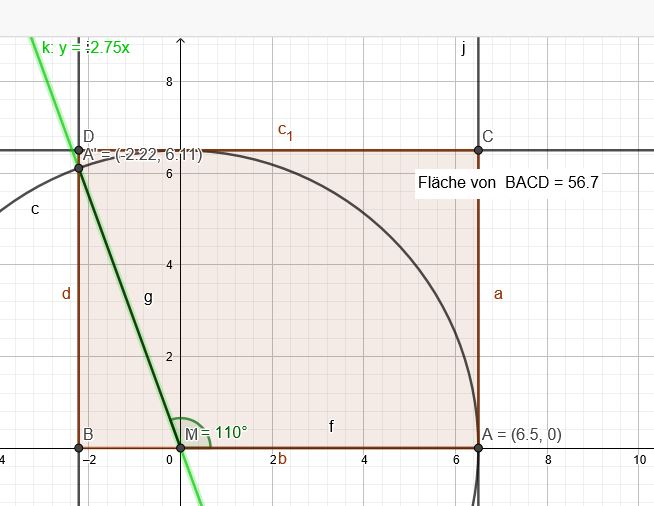
Geradengleichung durch MA´:
\(y=\tan(110°)x\) geschnitten mit \(x^2+y^2=6,5^2\):
\(x^2+\tan(110°)x^2=6,5^2\)
\(x_1≈-2,223\) 2. Wert entfällt.
Fläche des Rechtecks:
\(A=(|-2,223|+6,5) \cdot 6,5 ≈56,6995\mathrm{~dm^2} \)
c) Wieviel Prozent Abfall entstehen bei dem Rechteck aus Teilaufgabe b)?
Fläche es Kreisausschnitts:
\(A= \frac{110°}{360°} \cdot 6,5^2 \cdot π≈40,56 \mathrm{~dm^2} \)
Abfall: \(56,6995\mathrm{~dm^2}-40,56 \mathrm{~dm^2}=16,14\mathrm{~dm^2} \)
\(\frac{16,14}{56,6995}=\frac{x}{100}\)
\(x≈28,5\%\)