Nullstellen Berechnen durch Polynomdividion.

Question

Compito:

Conferma che f (x1) = 0. Calcola gli ulteriori zeri per divisione polinomiale.

Problema / approccio:

Qualcuno può aiutarmi?

Testo riconosciuto:

a) \ (f (x) = x ^ {3} +10 x ^ {2} +7 x-18; x_ {1} = 1 \)
c) \ (f (x) = x ^ {3} - 3 x ^ {2} -6 x + 18; x_ {1} = 3 \)

Answer 1

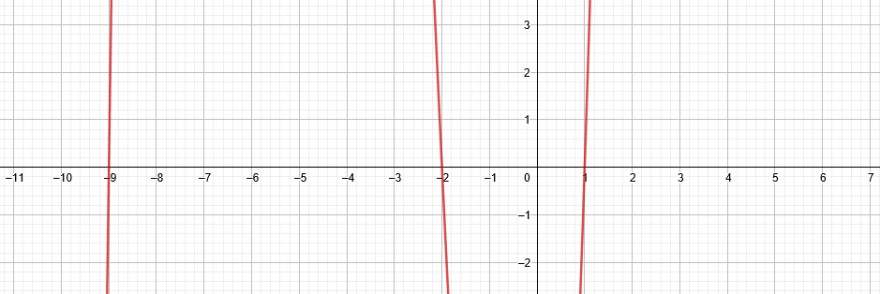
f(x)=x^3+10x^2+7x-18

f(1)=1^3+10*1^2+7*1-18=0

(x^3+10x^2+7x-18):(x-1)=x^2+11x+18                           x^2+11x+18=0

-(x^3-x^2)                                                                       x^2+11x=-18

-----------                                                                        (x+5,5)^2=-18+5,5^2=12,25

   11x^2+7x                                                                  x₂   =-5,5+\( \sqrt{12,25} \)=-2

                                                                                     x₃= -5,5-\( \sqrt{12,25} \)=-9

 -(11x^2-11x)

----------------------

             18x-18

           -(18x-18)

---------------------------

               0

Answer 2

a) $$f (x) = x ^ {3} +10 x ^ {2} +7 x-18; x_ {1} = 1 $$$$( x ^ {3} +10 x ^ {2} +7 x-18)/(x-1)=x^2+11x+18$$$$-(x^3-x^2)$$$$11x^2+7x$$$$-(11x^2-11x)$$$$18x-18$$$$-(18x-17)$$$$0$$$$f(x)=(x-1)(x+2)(x+9)$$$$x_1=1 \space ;\space x_2=-2 \space ;\space x_3=-9$$

c) $$f (x) = x ^ {3} - 3 x ^ {2} -6 x + 18; x_ {1} = 3 $$$$(x ^ {3} - 3 x ^ {2} -6 x + 18)/(x-3)=x^2-6$$$$-(x^3-3x^2)$$$$-(-6x+18)$$$$0$$$$f(x)=(x-3)(x^2-6)$$$$x_1=3 \space ;\space x_2=\sqrt{6} \space ;\space x_3=-\sqrt{6}$$

Comments

Antwort ergänzt.