Berechnen Sie die Kippachshöhe Hsp des Tachymeters auf dem Standpunkt SP und die Höhe HN des Neupunktes N.

Question

Von einem frei gewählten Standpunkt SP aus werden zu einem Anschlusspunkt A und zu einem Neupunkt N die Zenitwinkel z'i und die Schrägstrecken S'i mit einem elektronischen Tachymeter gemessen (Reflektorhöhe th = 1,50 m).

Der Anschlusspunkt A hat die Höhe HA = 237,153 mü. NN
Messwerte: ZA = 95,266 gon
                  S'A = 66,68 m

                  ZN = 107,302 gon
                  S'N = 35,274 m

Berechnen Sie die Kippachshöhe Hsp des Tachymeters auf dem Standpunkt SP und die Höhe HN des Neupunktes N. Zeichnen Sie zur Verdeutlichung des Rechenganges eine Ansichtsskizze.

Comments

Vom Duplikat:

Titel: "Hilfe" Berechnen Sie die Kippachshöhe Hsp des Tachymeters auf dem Standpunkt SP und die Höhe HN des Neupunktes N.

Stichworte: beweise,konvergenz,vektoren,harmonische-reihen,divergenz

Aufgabe:

…

Von einem frei gewählten Standpunkt SP aus werden zu einem Anschlusspunkt A und zu einem Neupunkt N die Zenitwinkel z'i und die Schrägstrecken S'i mit einem elektronischen Tachymeter gemessen (Reflektorhöhe th = 1,50 m).


Der Anschlusspunkt A hat die Höhe HA = 237,153 mü. NN
Messwerte: ZA = 95,266 gon
                S'A = 66,68 m

                ZN = 107,302 gon
                S'N = 35,274 m

Berechnen Sie die Kippachshöhe Hsp des Tachymeters auf dem Standpunkt SP und die Höhe HN des Neupunktes N. Zeichnen Sie zur Verdeutlichung des Rechenganges eine Ansichtsskizze.


Problem/Ansatz:

Könnte jemand bitte sagen wie wir diese Aufgabe lösen könnten.

Vielen Dank im voraus

Answer 1

Hallo,

das Problem bei diesen Aufgaben ist, dass kaum jemand weiß, was \(\text{gon}\), Zenitwinkel, Schrägstrecke und Reflektorhöhe ist. Ansonsten ist das ganze ziemlich einfache Trigometrie.

Nach meiner Einschätzung sollte die Skizze etwa so aussehen

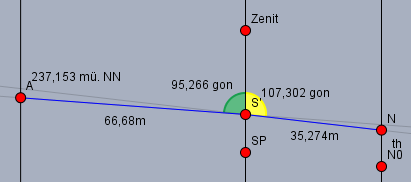
Berechnen Sie die Kippachshöhe Hsp des Tachymeters auf dem Standpunkt SP

Ich gehe davon aus, dass die 'Kippachshöhe Hsp' die Höhe des Punktes \(S'\) über NN ist. Dann ist $$\begin{aligned}Hsp &= HA - S'A \cdot \cos(ZA) \\&=237,153\,\text m - 66,68\,\text m \cdot \cos(95,266\,\text{gon}) \\&= 232,199\,\text m\end{aligned}$$

... und die Höhe HN des Neupunktes N

ich gehe hier davon aus, dass mit \(N\) der Reflektor selbst gemeint ist. Somit muss die Reflektorhöhe nicht berücksichtigt werden. Ansonsten muss man für den Standpunkt \(N_0\) von \(N\) noch die \(1,5\,\text m\) abziehen$$\begin{aligned}HN &= Hsp + S'N \cdot \cos(ZN) \\&= 232,199\,\text m + 35,274\,\text m \cdot \cos(107,302\,\text{gon}) \\&= 228,162\,\text m\end{aligned}$$

Comments

Vielen vielen Dank für Ihre Hilfe

---

Hallo Werner,

ich bin auch kein Geometer, hab aus der Aufgabenstellung

gelesen.

@Werner: Es wird doch von SP aus gemessen, oder? Was ist S' bei Dir?

---

Oh - die Ergebnisse stimmen nicht. Ich habe das korrigiert.

@wächter: jetzt stimmt zumindestens HN mit Deinem Ergebnis überein

Weiter bin ich davon ausggangen, dass bei jeder Messung ein Reflektor benöigt wird. Ich wüsste nicht, wie sonst die Abstandsmessung funktionieren sollte. Da von Standpunkt SP die Differenz zwischen A und N gemessen wird, spielt die Höhe des Reflektors keine Rolle. Es ist dabei egal, ob mit A und N die Reflektorhöhe oder die Höhe des jeweiligen Standpunkts gemeint ist.

Einzig bei der Höhe von Hsp kann das eine Rolle spielen. Da kommt es darauf an, wie genau HA definiert ist. Ich gehe aber davon aus, dass es sich dabei um die Höhe des Reflektors über NN handelt. Was anderes lese ich aus der Aufgabenstellung nicht. Zitat:

A hat die Höhe HA = 237,153 mü. NN

Ich unterscheide nur zwischen dem Standpunkt SP und der Position des Tachymeters S'. Da nur nach der Höhe des Tachymeters gefragt ist, spielt die Reflektorhöhe IMHO hier keine Rolle.

@Lokas: wäre nett, wenn Du uns dahingehend mal aufklärst. Ist A bzw. HA die Höhe des Reflektors über NN oder ist die (Mess-)Höhe des Reflektors HA+1,5m?

---

Ich hab diese Aufgabe von alten Klausuren, darf ich ein Bild davon hier schicken?

---

Morgen wird ich die Klausur schreiben, können Sie mir bitte sagen, welche die richtige Antwort ist ?

---

können Sie mir bitte sagen, welche die richtige Antwort ist ?

können wir erst, wenn Du uns sagst, wie das \(A\) bzw. das \(HA\) definert ist. (siehe meine Rückfrage im letzten Kommentar)

Das korrigierte Ergebnis in meiner Antwort ist IMHO korrekt, unter der Voraussetzung, dass die Reflektorhöhe für die Aufgabe irrelevant ist. Ob das so ist oder nicht, musst Du selber entscheiden. Das ist eine Frage der Definition von \(A\) und \(N\) bzw. \(HA\) und \(HN\)!

In der Zeichnung von wächter ist ein Fehler.

Dort steht für \(S'N\) \(ReN=(35,485, \dots\) in der Aufgabenstellung steht aber \(S'N=35,274\)

darf ich ein Bild davon hier schicken?

zeichen es ab und schicke ein Foto von der Zeichnung. Das ist auf jeden Fall ok.