Aufgabe: Gegeben ist die Funktion f mit f(x) = e^2*x , x e IR .
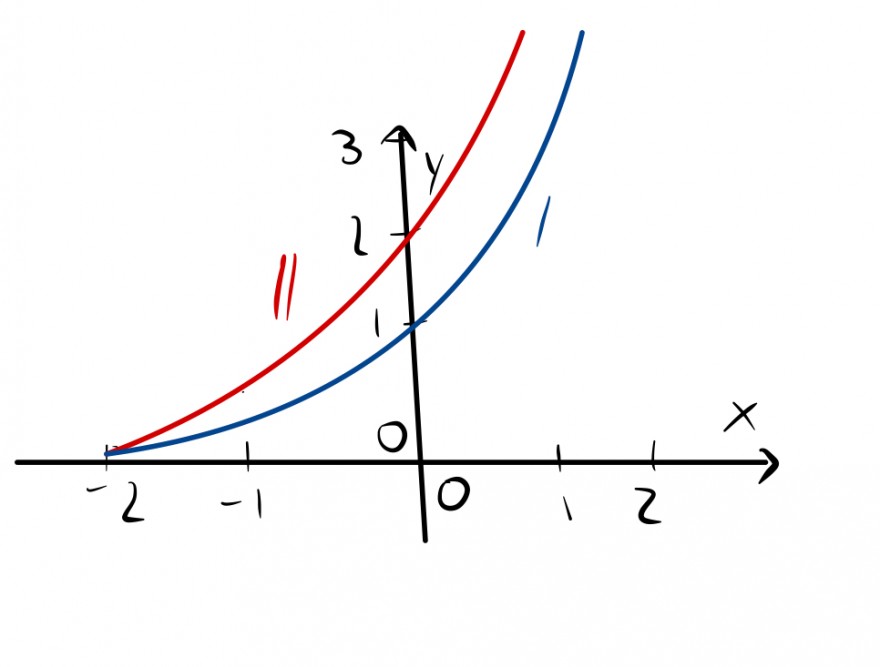
a)Die Abbildung zeigt die Graphen von f und f Entscheiden Sie, welcher der Graphen zu f gehört
Es ist g(x)=a f(X), a>0
Bestimmen Sie einen Wert für a so, dass der vertikale Abstand der beiden Graphen von g und g' an der Stelle x=0 denWert 3 hat.
Problem/Ansatz:
Ich verstehe die Aufgaben leider nicht. Ich habe versucht bei der ersten Aufgabe die Kettenregel anzuwenden, jedoch weiß ich nicht wie ich damit beweisen kann, welcher Graph zu der Funktion gehört.