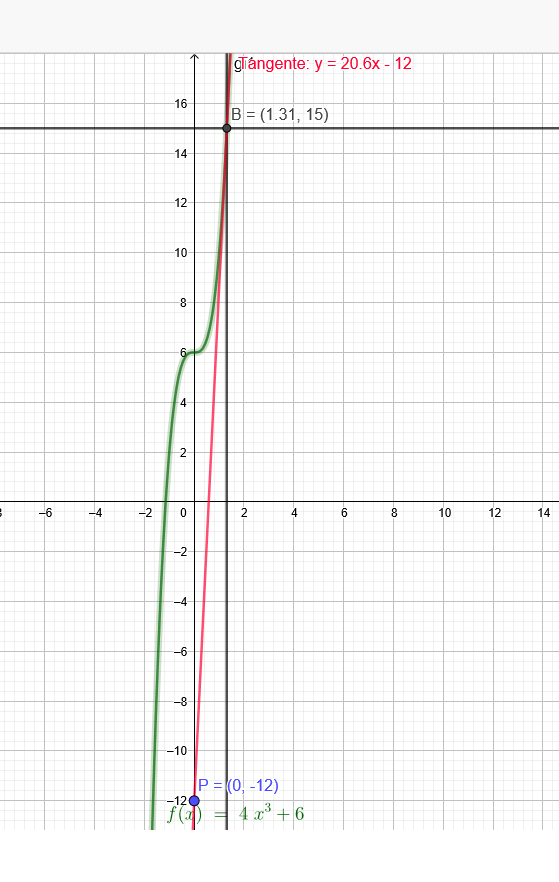
Bestimmen Sie den Berührpunkt der Tangente vom Punkt \( \mathrm{P}(0 \mid-12) \) an das Schaubild von \( f(x)=4 x^{3}+6 \)
Jetzt aber richtig: ( Ich bin durcheinander gekommen, weil eine 12 in der Ableitung und auch in P(0|-12) waren)
\( f(x)=4 x^{3}+6 \)
\( f(u)=4 u^{3}+6 \)
f´(x)=12x^2
f´(u)=12u^2
P(0|-12)
(4 u^3+6 +12) / u =12u^2
4 u^3+18=12u^3
8u^3=18
u^3=\( \frac{18}{8} \)=\( \frac{9}{4} \)=2,25
u=\( \sqrt[3]{2,25} \)
f(\( \sqrt[3]{2,25} \) ) =4*2,25+6=15