Hallo Alissa,
Ich habe Dir die Pyramide mal aufgeschnitten im Geoknech3D skizziert:
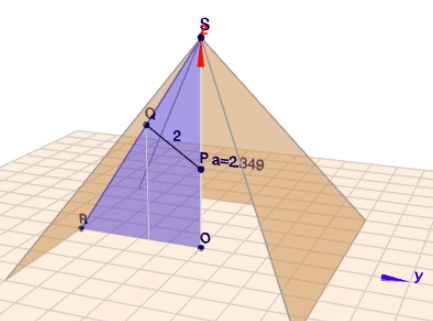
(klick auf das Bild, dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren)
Das blaue Dreieck \(\triangle ROS\) ist für die Berechnung von \(a\) relevant. Die Dreiecke \(\triangle ROS\) und \(\triangle PQS\) sind ähnlich. Folglich ist$$\frac{|SP|}{|PQ|} = \frac{|SR|}{|RO|} \implies |SP| = \frac{|SR| \cdot |PQ|}{|RO|}$$Es sind \(|PQ|=2\) und \(|RO|=4\). Und die Strecke \(|SR|\) berechnet sich nach Pythagoras$$|SR|= \sqrt{4^2 +6^2} = 2\sqrt{13}$$Dann ergibt sich$$|SP| = \frac{|SR| \cdot |PQ|}{|RO|} = \frac{ 2\sqrt{13} \cdot 2}{4} = \sqrt{13} \\ \implies a = |OP| = |OS|-|SP| = 6-\sqrt{13} \approx 2,349$$
Abstand des Koordinatenursprungs von den Seitenflächen?
funktioniert auch über die Ähnlichkeit im Dreieck \(\triangle ROS\).
Welcher der Punkte P hat außer von den Seitenflächen auch noch zur Grundfläche denselben Abstand?
Und in diesem Fall wäre \(|PQ|=|PO|\). Nehme die Gleichung für \(|SP|\) (s.o.) und setze \(|SP| + |PQ| = |SO| = 6\). Löse nach \(|PQ|\) auf.
Falls Du noch Fragen hast, so melde Dich bitte.