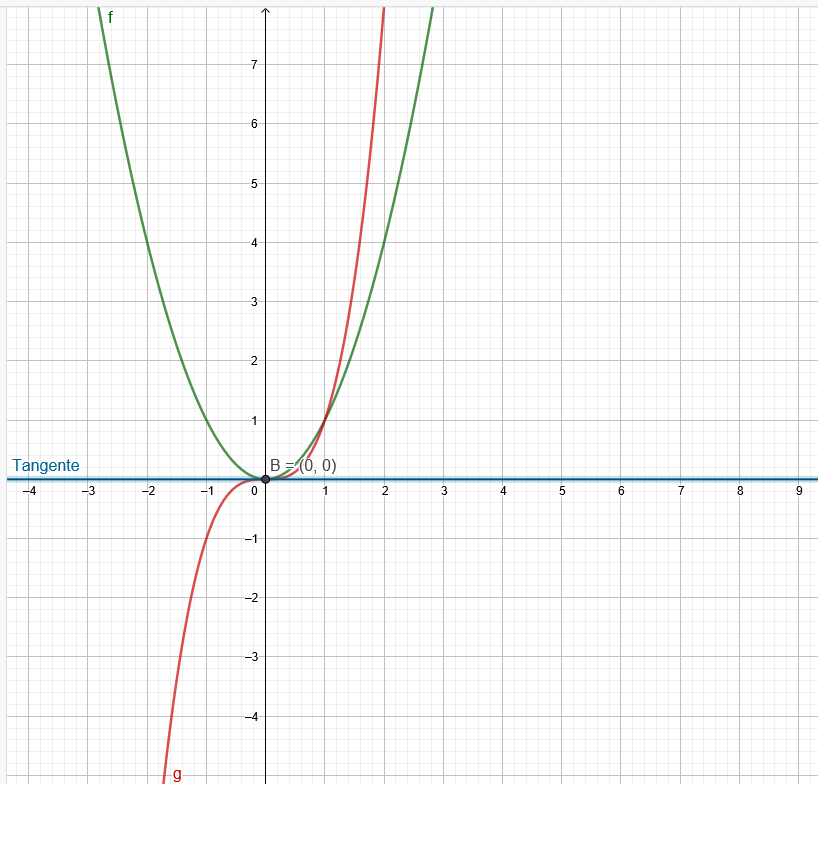
f(x)=x^2 und g(x)=x^3
f(u)=u^2 und g(v)=v^3
B1(u|u^2) B2(v|v^3)
f´(u)=2u und g´(v)=3v^2
Tangente an f(x) in B1: Tangente an g(x) in B2:
\( \frac{u^2}{u} \) =2u \( \frac{v^3}{v} \) =3v^2
u^2=2u^2 v^3 =3v^3
u=0 v=0
Hier sind die beiden Tangenten identisch. Ob es nun noch weitere Tangenten mit gleicher Steigung gibt entzieht sich meiner Kenntnis.