berechnen von Seitenlängen an einer Pyramide

Question

Die Cheopspyramide in Ägypten hat eine quadratische Grundfläche mit der Seitenlänge a=227m. Die Seitenkanten haben die Länge s=211m.

Text erkannt:

惟

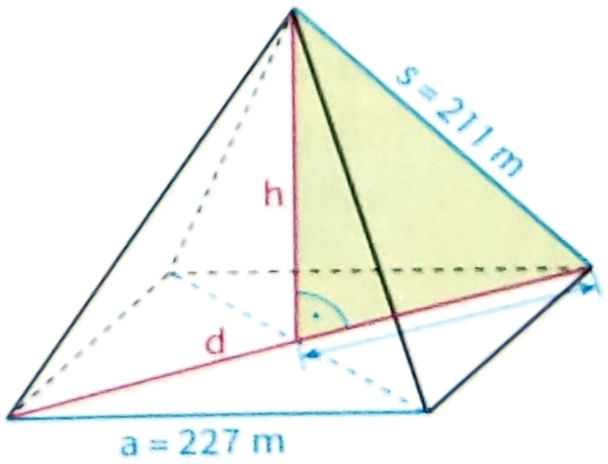
a) Berechne zunächst die Diagonalenlänge d der Grundfläche. Berechne dann die Höhe h der Cheopspyramide. Runde auf Meter.
b) Die Grundkante der Cheopspyramide war ursprünglich 230,3m, ihre Seitenkante 219,1m lang. Wie hoch war diese Pyramide ursprünglich?
c) Wie viel Prozent ist die Cheopspyramide heute niedriger als ursprünglich?

Bitte Rechenweg auch mit angeben
!

Answer 1

Hallo

Pythagoras kennst du? daraus die Länge der Diagonalen d  (Kontrolle 321m)

dann wieder Pythagoras in dem Dreieck mit d/2, h und s. Kontrolle (137m gerundet)

Gruß lul

Comments

Danke für deine Hilfe,

ich weiß bloß nicht so ganz, wie ich Pythagoras bei der Pyramide anwenden soll.

vielleicht kannst du mir das bitte etwas einfacher schreiben.

Paul

---

Hallo

die Rechtwinkligen Dreiecke mit halber Diagonale  Höhe und Seite sind da doch deutlich zu sehen? und dass im unteren Quadrat die Diagonale und die Seiten ein rechtwinkliges Dreieck bilden auch, Pythagoras ist immer in rechtwinkligen Dreiecken, ob die in ner Pyramide sind oder nicht ändert doch daran nichts?

rechtwinklige Dreiecke in Skizzen zu suchen muss man üben, aber hier hast du die ja schon angegeben?

lul