Skilanglauf (Modellierung von Exponentialfunktionen)

Question

Ich habe ein Problem bei mehrere Aufgaben :(

Meine Aufgabenstellung lautet: Der Verlauf einer Skilpoipe wird durch die Funktion f(x)=x*e^-x^2
modellhaft beschrieben. Von der Loipe zweigt im Punkt P(0/0)
tangential ein Weg ab, der zum Waldrand führt, welcher 1 km nördlich parallel zur x-Achse verläuft.

a) ich muss die Ableitungen f´und f´´ bestimmen, indem ich die Produkt- und die Kettenregel verwenden; und zeigen dass F(x)=1/2*e-x² eine Stammfunktion von f ist.

b) die Lage der beiden Extremalpunkte von f berechnen

Comments

Vom Duplikat:

Titel: Skiloipe (Modell. Exponentialfunktionen)

Stichworte: exponentialfunktion

Aufgabe:Eine Skiloipe hat die Funktion f(x)=x*e^-x^2 und Ableitungen f'(x) = e^(- x²)·(1 - 2·x²) und
f''(x) = e^(- x²)·(4·x3 - 6·x).

Ich muüsste noch folgendes ausrechnen und beschreiben können, aber habe sehr schlechte Mathe Kentnisse (also suche ich für Hilfe um es verstehen zu können):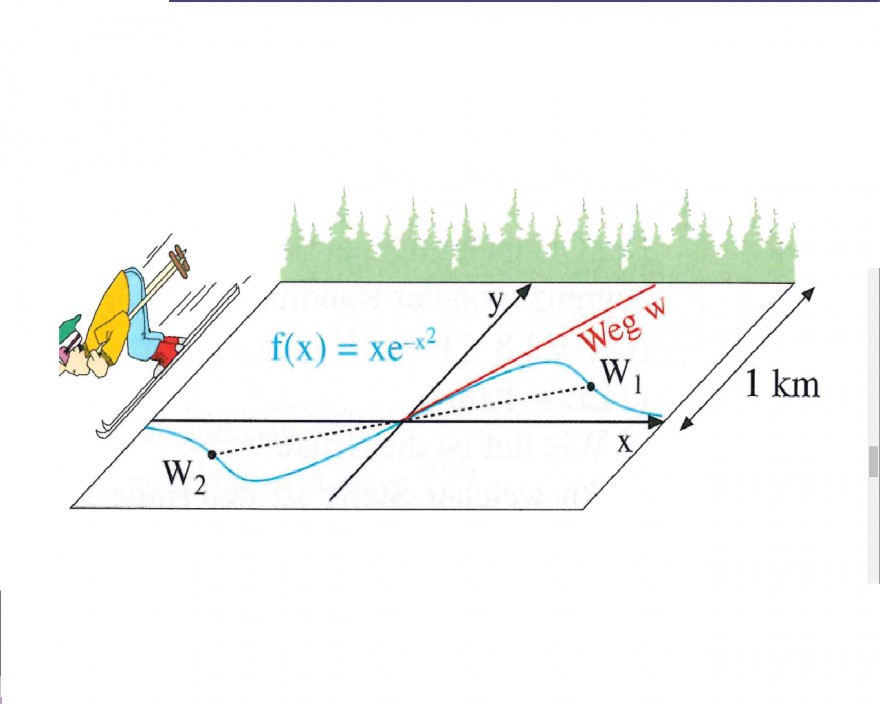

a) die Lage beiden Extremalpunkte der Skiloipe (wenn ich mich nicht irre) berechnen

b) die Gleichung und die Länge des zum Waldrand führenden Weges (w) bestimmen

c) die Länge des Weges zwischen Punkt W1 und W2 herausfinden, sowohl wie lange es dauert wenn man von einem Punkt zum anderen laufen würde und zwar in die Geschwindigkeit von 20km/h.

Answer 1

f(x) = x·e^(- x^2)

f'(x) = e^(- x^2)·(1 - 2·x^2)

f''(x) = e^(- x^2)·(4·x^3 - 6·x)

F(x) = 0.5·e^(- x^2)

F'(x) = - x·e^(- x^2)

Damit ist F(x) keine Stammfunktion. Prüf das mal ob es eventuell F(x) = -1/2·e^(- x^2) lautet.

Comments

Ja, es lautet F(x) = -1/2·e^(- x²)

---

Können Sie mir vielleicht erklären, warum es keine Stammfunktion ist?

---

Nur wenn du das Minus vergisst, ist es keine Stammfunktion. Mit dem Minus ist es eine Stammfunktion.