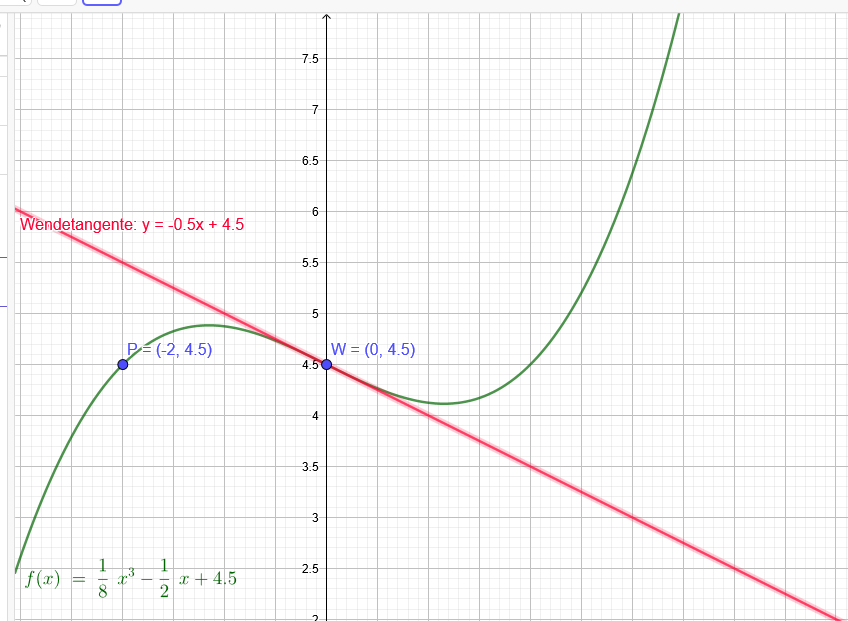
1.Die Funktion ist eine ganz rationale Funktion 3. Grades.
f(x)=a*x^3+b*x^2+c*x + d
2. Der Wendepunkt liegt bei (0|4,5)
f(0)=a*0^3+b*0^2+c*0 + d
1.)d=4,5
3. Steigung der Wendetangente -0.5
f´(x)= 3a*x^2+2b*x + c
f´(0)= 3a*0^2+2b*0+ c
2.)c=-0,5
Wendepunkt y´´ = 0
f´´(x)= 6a*x+2b
f´´(0)= 6a*0+2b
2b=0
3.)b=0
f(x)=a*x^3-0,5x +4,5
4. y-Wert an der unteren Flächengrenze ist gleich dem Y-Werts des Wendepunktes Intervall von -2 bis 3
P(-2|4,5)
f(-2)=a*(-2)^3-0,5*(-2) +4,5
a*(-2)^3-0,5*(-2) +4,5=4,5
-8a+1=0
a=\( \frac{1}{8} \)
f(x)=\( \frac{1}{8} \)*x^3-0,5x +4,5