Hallo,
Eine ganzrationale Funktion ist
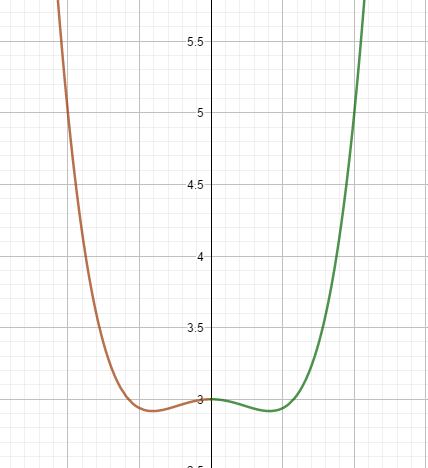
- achsensymmetrisch bezüglich der y-Achse, wenn die x-Terme nur in geraden Potenzen im Funktionsterm vorkommen.
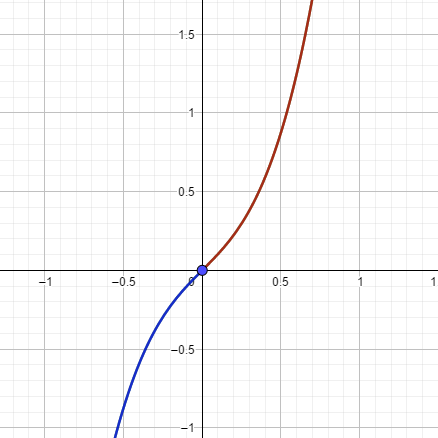
- punktsyymetrisch bezüglich des Ursprung, wenn die x-Terme nur in ungeraden Potenzen im Funktionsterm vorkommen und f(x) kein konstantes Glied enthält.
punktsymmetrisch zum Ursprung
würdest du den Teil des Graphen bis zum Ursprung an diesem spiegeln, erhältst du das Gegenstück im gegenüberliegenden Quadranten
achsensymmetrisch zur y-Achse
spiegelst du die rechte Seite des Graphen an der y-Achse, erhältst du die linke Seite