f(x)=\( \frac{1}{6} \) x²(x-6)=\( \frac{1}{6} \)*\( x^{3} \) - \( x^{2} \)

Text erkannt:
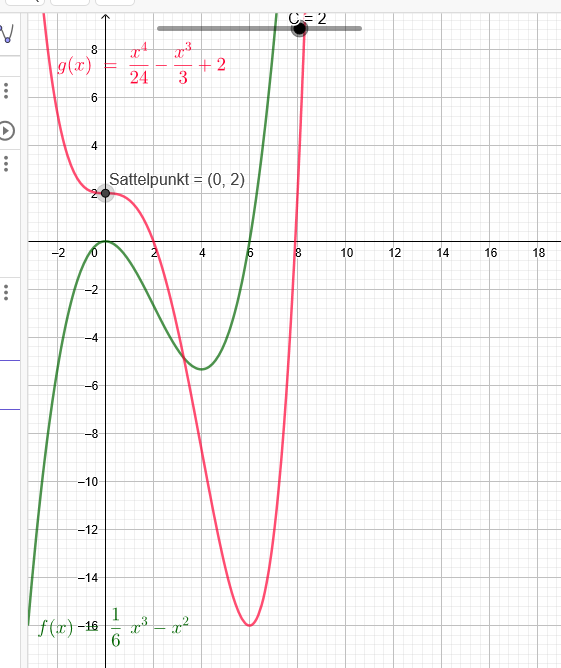
\( f(x)=\frac{1}{6} x^{3}-x^{2} \) (ist in grün gezeichnet)
\( F(x)=\int\left(\frac{1}{6} x^{3}-x^{2}\right) \cdot d x=\frac{1}{6} \cdot \frac{x^{4}}{4}-\frac{1}{3} x^{3}=\frac{x^{4}}{24}-\frac{x^{3}}{3}+C \)
\( F(x)=\frac{x^{4}}{24}-\frac{x^{3}}{3}+C \)
\( F^{\prime}(x)=\frac{1}{6} x^{3}-x^{2} \) (ist in rot gezeichnet)
\( \frac{1}{6} x^{3}-x^{2}=0 \)
\( x^{2} \cdot\left(\frac{1}{6} x-1\right)=0 \)
\( x_{1,2}=0 \)
\( x_{3}=6 \)
Art des Extremwertes:
\( F \cdot(x)=\frac{1}{2} x^{2}-2 x \)
\( F^{\prime} \cdot(0)=\frac{1}{2} \cdot 0-2 \cdot 0=0 \)
Hier liegt ein Sattelpunkt (wagerechte Tangente) ( ist kein Extremwert)
\( F^{\prime} \cdot(6)=\frac{1}{2} \cdot 6^{2}-2 \cdot 6=6>0 \) Minimum