Berechne für beide Fälle die Gesamtlänge der Zufahrtstraßen.

Question

Hallo,

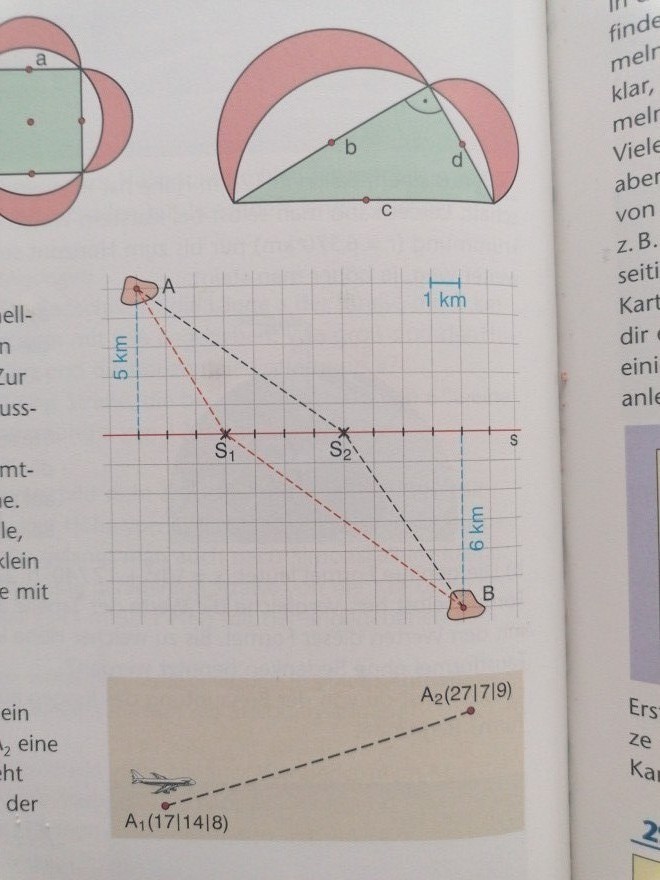
Ich habe eine Hausaufgabe aufbekommen(Skizze in der Mitte mit den Punkten A und B). Ich verstehe nicht wie ich die Folgenden Aufgaben lösen soll.

Aufgabe:

Die Orte A und B sollen einen gemeinsamen Anschluss an die Schnellstraße s erhalten. Die Zufahrtstraßen können geradlinig gebaut werden. Zur Diskussion stehen S1 und S2

a) Berechne für beide Fälle die Gesamtlänge der Zufahrtstraßen.

Würde mich über Hilfe sehr freuen:)

Danke

…

Problem/Ansatz:

Answer 1

AS₁B=\( \sqrt{3^2+5^2} \)+\( \sqrt{6^2+8^2} \)≈15,83 km

AS₂B=\( \sqrt{7^2+5^2} \)+\( \sqrt{6^2+4^2} \)≈15,81 km.      

Answer 2

AS1= √(3^2+5^2) = 4

S1B = √(6^2+8^2) = 10

--> Gesamtlänge 14 km

Die 2. geht genauso.

Comments

√34=4 ?

Da hast du dich etwas verrechnet.

:-)

Answer 3

Die Punkte A, S₁ und der Punkt S_A wo die blaue Strecke von A auf s trifft bilden ein rechtwinkliges Dreieck.

Verwende den Satz des Pythagoras. um AS₁ zu berechnen.