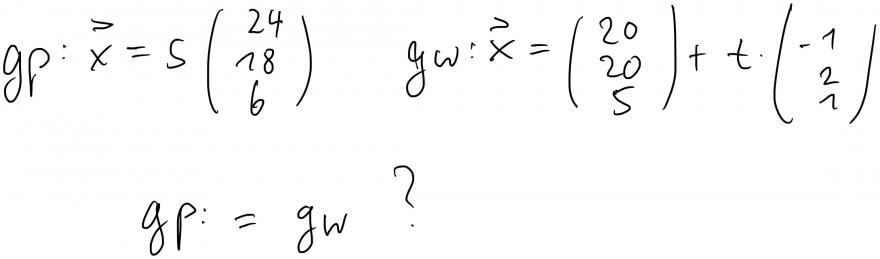Aufgabe:
Im Sonnensystem ist ein rechtwinkliges Koordinatensystem platziert. Dabei entspricht der
Koordinatenursprung der Sonne und die xy -Ebene stellt die sogenannte Ekliptik dar. Der Zwergplanet Pluto
befindet sich zum Zeitpunkt t = 0 im Punkt P (24 |18 | 6) und bewegt sich um die Sonne in der Bahnebene
E P . In dieser Ebene liegt die Gerade gP , die Sonne und Pluto verbindet.
Eine Weltraumsonde bewegt sich näherungsweise auf der Geraden gW : x =(20|20|5) t(-1|2|1)
Der Parameter t in der obigen Geradengleichung von gW steht für die Zeit in Jahren.
Alle Koordinaten sind in Astronomischen Einheiten angegeben (1 AE = mittlerer Abstand zwischen Sonne
und Erde).
a)
Geben Sie eine Gleichung der Geraden g P in Parameterform an.
Zeigen Sie, dass die Geraden g P und g W windschief sind.
Problem/Ansatz:
Ich muss die beiden Geraden gleich setzen richtig?
Wie gehe ich dann vor? Ich setze die Gl.1= s und Gl.2 = t
Dann setze ich s und t in die Gl.3 ?