Analytische Geometrie schiefes Prisma

Question

Aufgabe:

In einem kartesischen Koordinatensystem sind die Punkte A (2/1/-1) B (6/4/-2) C (1/3/1) F (4/6/4) und H (-1/5/7) gegeben Die Punkte A B C D E F G und H sind Eckpunkte eines schiefen Prismas mit der Grundfläche ABCD

a) Geben Sie die Koordinaten der Punkte G und E an

b) Weisen Sie nach, dass die Grundfläche des Prismas ein Rechteck ist

c) Untersuchen Sie ob sich alle Raumdiagonalen des Prismas in genau einem Punkt schneiden. Berechnen Sie gegebenenfalls die Koordinaten des Schnittpunktes dieser Diagonalen.

Text erkannt:

(1)

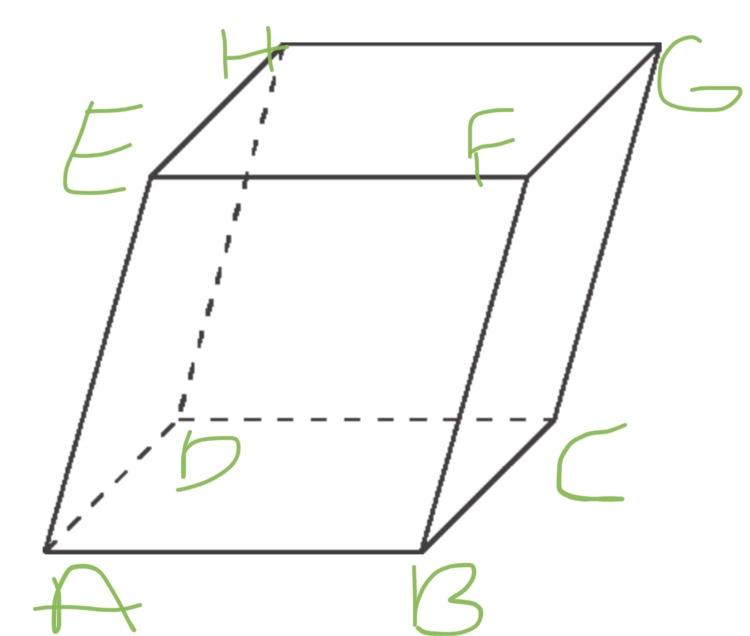
So sieht die Abbildung ungefähr aus

Problem/Ansatz:

Kann mit bitte jemand bei der Aufgabe helfen es können auch nur Erklärungen sein damit ich weiß was genau ich da machen soll.

Answer 1

\( \vec{BF} \)=\( \begin{pmatrix} -2\\2\\6 \end{pmatrix} \)

\( \vec{OC} \)+\( \vec{BF} \)=\( \vec{OG} \)

\( \begin{pmatrix} 1\\3\\1 \end{pmatrix} \)+\( \begin{pmatrix} -2\\2\\6 \end{pmatrix} \)=\( \begin{pmatrix} -1\\5\\7 \end{pmatrix} \).

G(-1|5|7).