b) f(x) = t·x² - x - 1
Nullstellen:
t • x^2 - x - 1=0
t • x^2 - x =1 | : t
x^2 - \( \frac{1}{t} \) x =\( \frac{1}{t} \)
( x - \( \frac{1}{2t} \))^2 = \( \frac{1}{t} \) +\( \frac{1}{4t^2} \) =\( \frac{4t+1}{4t^2} \)
x₁= \( \frac{1}{2t} \)+\( \frac{1}{2t} \)•\( \sqrt{4t+1} \)
x₂=\( \frac{1}{2t} \)-\( \frac{1}{2t} \)•\( \sqrt{4t+1} \)
Diskriminante =0 gibt eine Nullstelle : ( Hochpunkt)
4t+1=0 → t = -\( \frac{1}{4} \)
4t+1>0 → t >- \( \frac{1}{4} \) ergibt 2 Nullstellen, aber für t=0 gibt es eine Gerade , für t=\( \frac{1}{4} \) ist dort nur eine Nullstelle, ist ein Tiefpunkt.
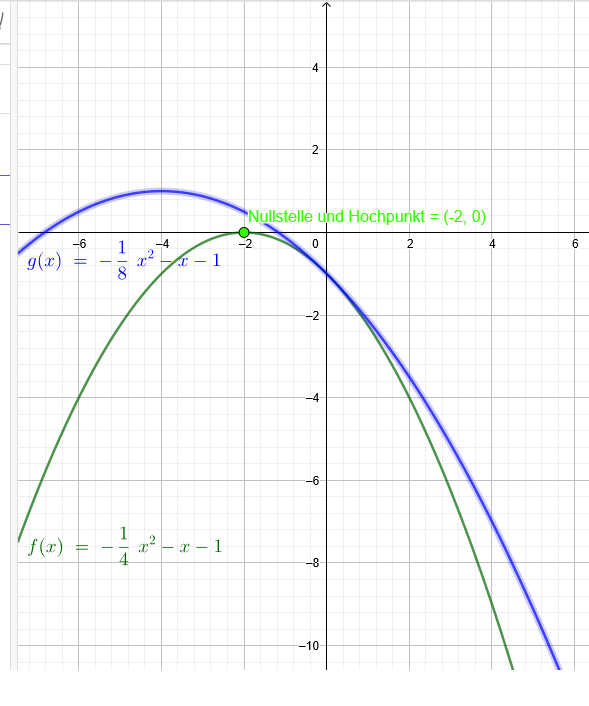
1.) t= -\( \frac{1}{4} \) N(-2|0)
f(x) = -\( \frac{1}{4} \)*x^2 - x - 1 in grün gezeichnet
2.) t= - \( \frac{1}{8} \)
g(x)= -\( \frac{1}{8} \)*x^2 - x - 1 in blau gezeichnet