Aufgabe 1: Gegeben ist die Funktion f mit f(x) = 1/5 x^2
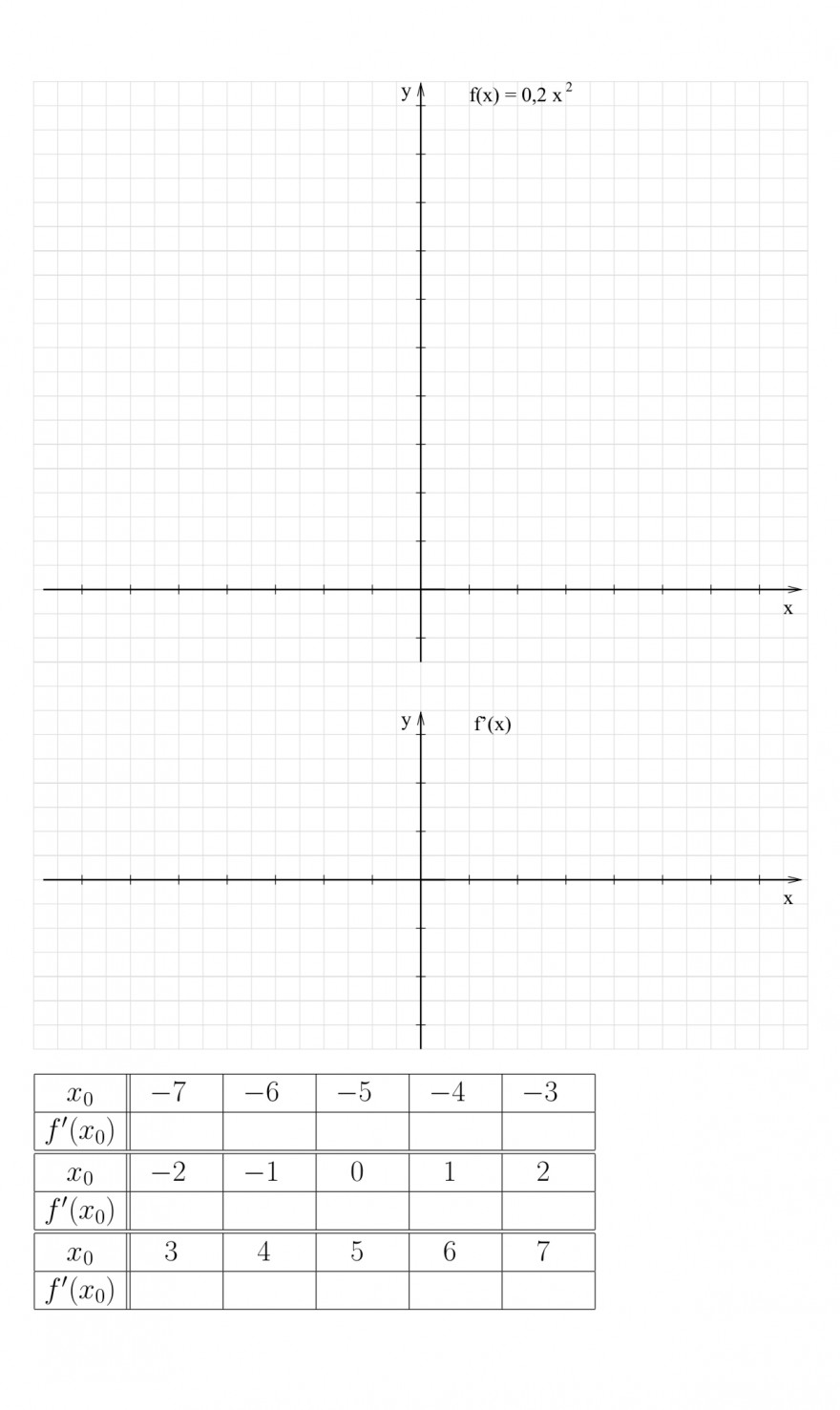
a) Zeichnen Sie den Graph von f im Intervall −7 ≤ x ≤ 7 in ein Koordinatensystem.
b) Bestimmen Sie anhand der Zeichnung die Ableitungen an den Stellen x0 = −7, x0 = −6, x0 = −5, . . ., x0 = 7. Tragen Sie die Ergebnisse in eine Tabelle ein.
c) Tragen Sie die Wertepaare aus Aufgabenteil b) in ein Koordinatensystem ein. Dieses Koordi- natensystem sollte genau unterhalb des Koordinatensystems aus Aufgabenteil a) stehen.
Aufgabe 2:
Für die Vereinfachung der Differenzenquotienten ist der sichere Umgang mit den binomischen Formeln wichtig. Wenn im Funktionsterm höhere Potenzen von x vorkommen, müssen auch Terme der Form (x0 + h)^3 oder (x0 + h)^4 ausmultipliziert werden. Diese Terme werden dann länger.
a) Schreibe den Term(a+b)^3 ohne Klammern. Tipp: (a+b)^3 =(a+b)^2·(a+b).
b) Schreibe den Term (a + b)^4 ohne Klammern.
Text erkannt:
| 1 1 1