Hallo Rieke,
A) p= 17,5 cm Beta= 66 Grad
mache Dir immer eine Skizze. Diesmal sähe die so aus:
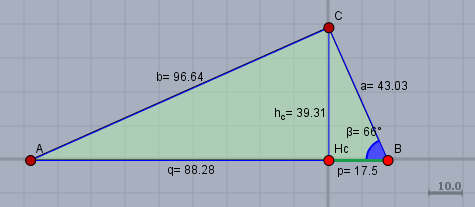
Im Dreieck \(H_cBC\) kann man ablesen
$$ \tan \beta = \frac {h_c}p \\ \implies h_c = p \cdot \tan \beta = 17,5 \cdot \tan(66°) \approx 39,3$$Nach dem Höhensatz ist$$h_c^2 = p \cdot q \\ \implies q = \frac{h_c^2}{p} = \frac{(p \cdot \tan \beta)^2}{p} = p \cdot (\tan \beta)^2 = 17,5 \cdot (\tan (66°))^2 \approx 88,3$$\(c\) ist die Summe aus \(p\) und \(q\) - das schaffst Du alleine. Weiter ist$$\sin \beta = \frac bc \\ \begin{aligned} \implies b &= c \cdot \sin \beta = (p+q)\cdot \sin \beta = p(1 + (\tan \beta)^2) \sin \beta \\&= 17,5 \cdot (1 + (\tan(66°))^2) \cdot \sin(66°) \approx 96,6\end{aligned}$$ und zum Schluß$$\cos \beta = \frac ac \\ \begin{aligned}\implies a &= c \cdot \cos \beta = p(1 + (\tan \beta)^2) \cdot \cos \beta \\ &= 17,5 \cdot (1 + (\tan(66°))^2) \cdot \cos(66°) \approx 43,0\end{aligned}$$
B) h= 145 mm Beta= 42,8 Grad
Skizze .. die dient dann nachher auch zur Kontrolle der Ergebniss
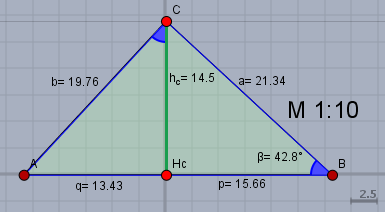
Im Dreieck \(\triangle H_cBC\) gilt wieder $$\tan \beta = \frac {h_c}p \\ \begin{aligned} p &= \frac{h_c}{\tan \beta} = \frac{145}{\tan(42,8°)} \approx 156,6 \end{aligned}$$Es folgt der Höhensatz $$ h_c^2 = pq \\ \begin{aligned} \implies q &= \frac{h_c^2}p = \frac{h_c^2}{\frac{h_c}{\tan \beta}} = h_c \cdot \tan \beta \\&= 145 \cdot \tan(42,8°) \approx 134,3 \end{aligned}$$Es geht weiter im Dreieck \(\triangle AH_cC\) mit \(b\) und im Dreieck \(\triangle H_cBC\) mit \(a\)$$\triangle AH_cC: \quad \cos \beta = \frac {h_c}b \\ \begin{aligned}\implies b &= \frac {h_c}{\cos \beta} \\&= \frac{145}{\cos(42,8°)} \approx 197,6\end{aligned} \\ \triangle H_cBC: \quad \sin \beta = \frac {h_c}{a} \\ \begin{aligned} \implies a &= \frac{h_c}{\sin \beta} \\&= \frac{145}{\sin(42,8°)}\approx 213,4\end{aligned}$$