Wert einer Gegebenen Reihe bestimmen

Question

Aufgabe:

Ich soll den Wert der Reihe bestimmen. Eigentlich bringen wir die Reihe immer in die Form der geometrischen Reihe, hier bekomme ich das aber nicht hin.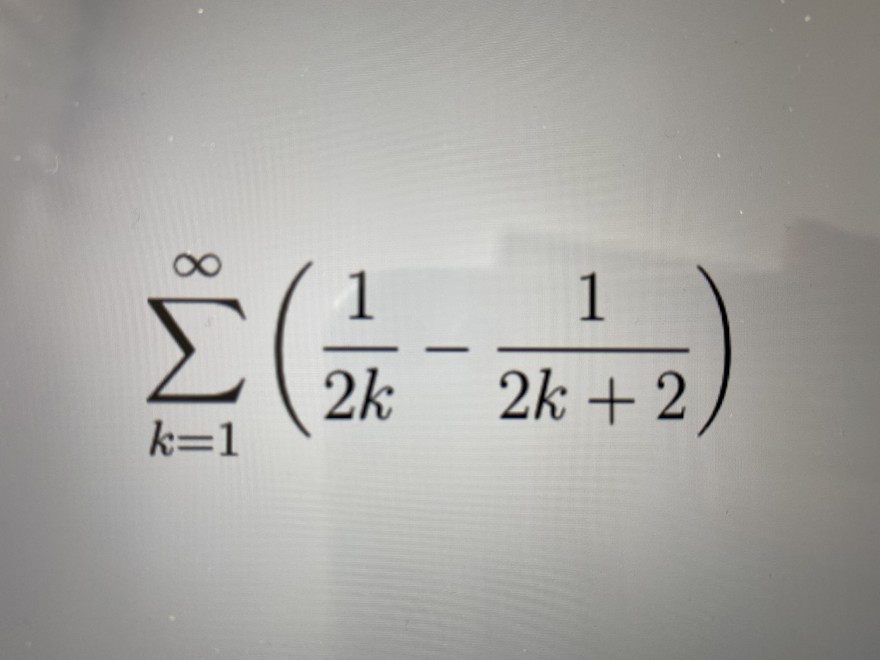

Text erkannt:

\( \sum \limits_{k=1}^{\infty}\left(\frac{1}{2 k}-\frac{1}{2 k+2}\right) \)

Answer 1

Zeige zunächst durch vollständige Induktion \(\sum \limits_{k=1}^{n}\left(\frac{1}{2 k}-\frac{1}{2 k+2}\right) \)=\( \frac{n}{2(n+1)} \)

und bilde dann den Grenzwert für n→∞.

Comments

Hallo,

fehlt auf der rechten Seite nicht noch etwas?

Gruß

---

Ja, danke. Wurde nachgetragen. (Schreibfehler)