Question

Habe ich das richtig gemacht? Wie kann ich jetzt weiter mit Umfang und Fläschcheneinhalt

Text erkannt:

(1) winkel
9
\( 20^{2}-29^{2}=\sqrt{ }=21 \mathrm{~cm} \)
\( \tan \beta=\frac{20}{10.29}=0,68 \)
\( \beta=34,6^{\circ} \)
\( 180-90-34,6=55,4 \)
\( U= \)
\( A= \)

Answer 1

Hallo Vemon,

mache Dir eine Zeichnung und kontrolliere Deine Ergebnisse an Hand der Zeichnung. Ich nehme mal an, dass Die Hypotenuse \(c=29\) und die Kathete \(b=20\) gegeben waren.

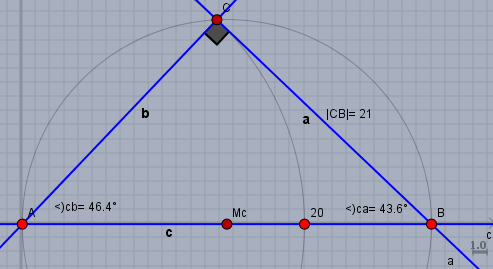
Die Kathete \(a\) hast Du mit \(a=\sqrt{29^2-20^2} = 21\) richtig ausgerechnet. Für den Winkel \(\beta\) gilt aber:$$\sin \beta = \frac{b}{c} = \frac{20}{29} \implies \beta \approx 43,6°$$und \(\alpha\) ist dann im rechtwinkligen Dreieck schlicht \(\alpha = 90°-\beta\).

Wie kann ich jetzt weiter mit Umfang und Fläschcheneinhalt

Für den Umfang addiere die drei Seiten$$U = a + b + c = 21 + 20 + 29 = 70$$und für den Flächeninhalt \(F\) brauchst Du beim rechtwinkligen Dreieck nur die Katheten mit einander zu multiplizieren:$$F = \frac 12 a b = \frac 12 \cdot 21 \cdot 20 = 210$$

Comments

Ich dankkeee sehrerr ich habe das gut verstanden dankee

Answer 2

1. Es muss \( \sqrt{29^2-20^2} \)=21 heißen.

2. tan(β)=20/21 und β≈43,6°,dann ist α≈46,4°.

U=29+21+20=70

A=21·20/2=210.