b)
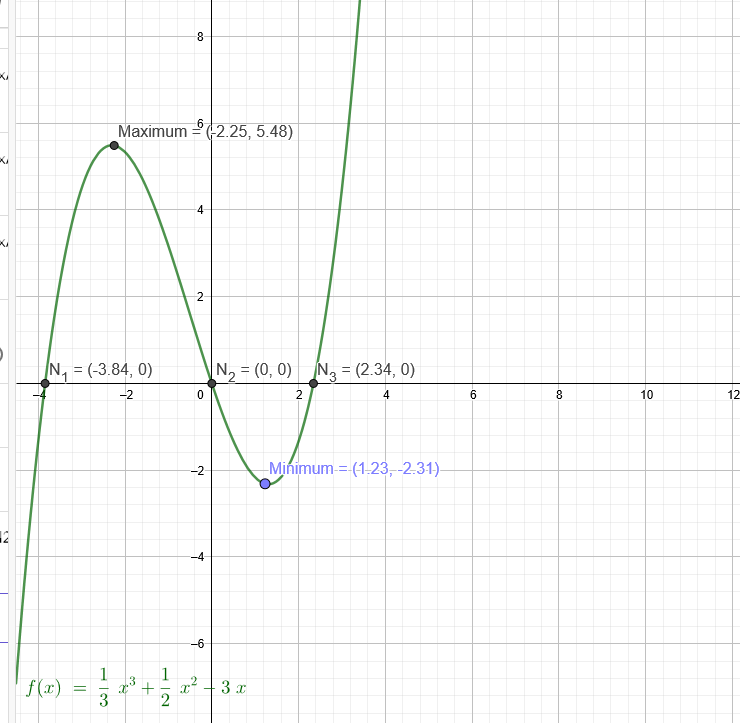
f(x)=\( \frac{1}{3} \) *x^3+\( \frac{1}{2} \) *x^2-3x
1.) Nullstellen f(x)=0
\( \frac{1}{3} \) *x^3+\( \frac{1}{2} \) *x^2-3x=0
x*(\( \frac{1}{3} \) *x^2+\( \frac{1}{2} \) *x-3)=0
x₁=0
\( \frac{1}{3} \) *x^2+\( \frac{1}{2} \) *x-3=0|*3
x^2+\( \frac{3}{2} \)*x=9
(x+\( \frac{3}{4} \))^2=9+\( \frac{9}{16} \)=\( \frac{153}{16} \)|\( \sqrt{} \)
1.) x+\( \frac{3}{4} \)=\( \frac{1}{4} \)*\( \sqrt{153} \)
x₁=...
2.) x+\( \frac{3}{4} \)= - \( \frac{1}{4} \)*\( \sqrt{153} \)
x₂=...
2.) Lokale Extrema f´(x)=0
f´(x)=x^2+x - 3
x^2+x =3
(x+\( \frac{1}{2} \) )^2=3+(\( \frac{1}{4} \))^2=\( \frac{49}{16} \)|\( \sqrt{} \)
1.) x+\( \frac{1}{2} \)=\( \frac{7}{4} \)
x₁=\( \frac{5}{4} \) f(\( \frac{5}{4} \))=...
2.) x+\( \frac{1}{2} \)= -\( \frac{7}{4} \)
x₂=-\( \frac{9}{4} \) f(-\( \frac{9}{4} \))=...
Art der Extremwerte:
f´´(x)=2x+1
f´´(\( \frac{5}{4} \) )=2*\( \frac{5}{4} \) +1>0 Minimum
f´´(-\( \frac{9}{4} \) )=2*(-\( \frac{9}{4} \) )+1<0 Maximum