Wie berechne ich die Parameter n und p bei einer binomialverteilten Zuffalsgröße?

Question

Aufgabe:

Wie berechne ich die Parameter n und p bei einer binomialverteilten Zuffalsgröße?

Problem/Ansatz:

bei der Aufgabe muss ich zu n (Anzahl Dürchführungen) und p (Trefferwahrscheinlichkeit) mögliche Parameter angeben. Es liegt ein Glockenförmiger Graph vor (das Maximum ist bei x=15 und y=14).

Ich würde mich über Lösungsvorschläge freuen.

Comments

Ohne den Graphen zu sehen sind Antworten notgedrungen sehr spekulativ.

Answer 1

Was heißt denn y = 14 ? Soll das 14% heißen?

Comments

Die Einheiten von der x- und y-Achse sind nicht angegeben. Da man mögliche Parameter angeben soll, denke ich, dass man die Einheit (ob das Prozent sein könnte oder nicht) selber definieren darf. Der Extrempunkt (Maximum) muss aber bei H (15/14) sein.

---

Dann würde ich es einfach durch eine Normalverteilung annähern, die E(x)=15 und eine beliebige Standardabweichung hat. Dann kannst du das p in der Tabelle nachlesen.

---

Die Einheiten von der x- und y-Achse sind nicht angegeben. Da man mögliche Parameter angeben soll, denke ich, dass man die Einheit (ob das Prozent sein könnte oder nicht) selber definieren darf. Der Extrempunkt (Maximum) muss aber bei H (15/14) sein.

Dann trifft meine obige Verteilung zu. Dort sind es nur 14% = 0.14 in der üblichen Achsenskalierung.

Du könntest recht einfach eine Exceltabelle machen die zu jedem n das p passend wählt, sodass der Erwartungswert bei 15 liegt. Mittels der Binomialverteilung kannst du dann auch jeweils die WK berechnen das die WK für genau 15 Treffer bei 14% liegt.

Die Tabelle könnte man auch mit vielen Taschenrechnern für die Oberstufe machen.

---

Die Exceltabelle würde wie folgt aussehen

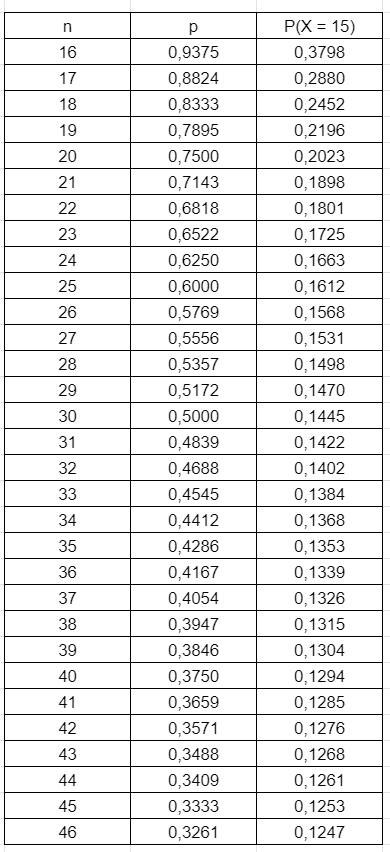
Man kann auch die Werte über die Normalverteilung nähern. Dann müsste gelten

n·p = 15
1/√(2·pi·n·p·(1 - p)) = 0.14

Das ist ein Gleichungssystem welches man lösen kann. Ich komme beim Lösen auf: n = 32.70 ∧ p = 0.4587

In dieser Umgebung sollte man mit der Binomialverteilung also nochmals nachrechnen.

Damit kommt man dann noch etwas schneller auf den Bereich. So hatte ich es übrigens zunächst gemacht.