Volumen der Knickpyramide von Snofru berechnen

Question

Aufgabe: Bei der Knickpyramide des Snofru wird auf einem Quadrat mit 189 m Seitenlänge zunächst bis auf eine Höhe von 49 m mit einem Neigungswinkel von 43 grad bis zur Spitze in ursprünglich 104 m Höhe weiter gebaut. Nimm an, dass die Pyramide vollständig aus Stein besteht und berechne das Volumen der insgesamt verbauten Steine.

Hinweis: Die Neigungswinkel ist der Winkel, der von den Seitenflächen mit der Grundfläche eingeschlossen wird. Nutze die Trigonometrie in einem rechtwinkligen Dreieck.

Komme mit der Aufgabe leider nicht klar und würde mich sehr über Antworten freuen:)

Answer 1

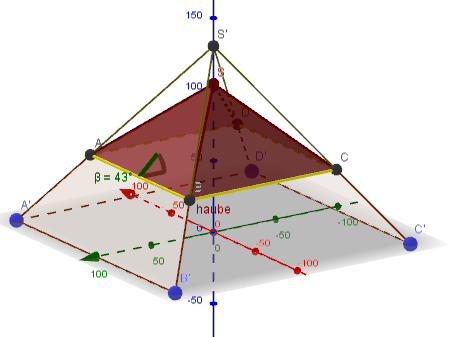
Die Pyramidenhaube ABCDS mit 43° Seitenneigung hat eine Grundfläche in

49 m höhe mit einer Seite von s=2(104 - 49) / tan(43°) =~ 117.961

und ein Volumen von Phaube = 1/3 G*h =~255102.71

Darunter die GrundPyramide A'B'C'D'. In einem geeigneten KO def

A=(s / 2, s / 2, 49), C=((-s) / 2, (-s) / 2, 49)

A'=(189 / 2, 189 / 2, 0) , C'=(-189 / 2, -189 / 2, 0)

die Geraden AA' x BB' schneiden sich in einer nie erreichten Spitze von S'=~(0,0,130.364)

Pyramidenstumpf, Grundpyramide = 1/3*189^2*130.364 - 1/3 s^2 (130.364-49) = ~1174860.566