Allgemeine quadratische Funktionen. f: x --> 9x^2 - 12x - 5 Kleinsten Funktionswert bestimmen.

Question

Ich verstehe das nicht, bitte mit Rechenweg:

Bestimme den kleinsten Funktionswert der quadratischen Funktion:

a) f: x --> 3x² + 12x - 25

b) f: x --> 9x² - 12x - 5

Comments

Bitte antworten! Ich komme einfach nicht weiter und muss für eine Schulaufgabe lernen! :(

Answer 1

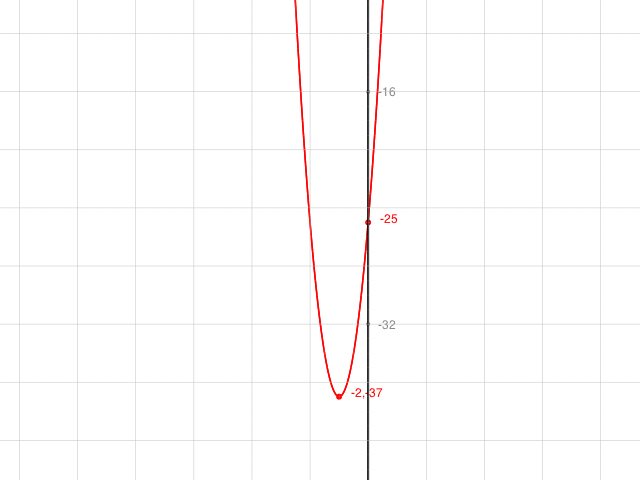
a) f: x --> 3x² + 12x - 25

= 3(x^2 + 4x) -25            |quadr. ergänzen
=3(x^2 + 4x + 4 -4) - 25      
=3((x+2)^2 - 4) - 25
=3(x+2)^2 - 12 - 25
=3(x+2)^2 - 37
S(-2,-37)

da 3> 0 ist die Parabel nach oben geöffnet.

y=-37 ist der kleinste y-Wert, den die Funktion annehmen kann.

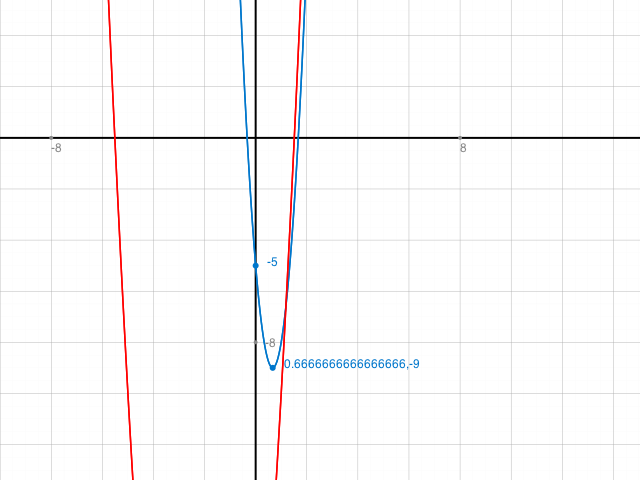
b) f: x --> 9x² - 12x - 5
=9(x^2 - 12/9 x         )-5            
=9(x^2 -4/3x      )-5         |quadr. ergänzen
=9(x^2 -4/3 x + (2/3)^2  - (2/3)^2)-5
=9((x-2/3)^2 - 4/9) -5
=9(x-2/3)^2 - 4 - 5

=9(x-2/3)^2 - 9

S(2/3, -9).   9>0. Parabel nach oben geöffnet.

y=-9 ist der kleinste y-Wert, den die Funktion annehmen kann.
 

Du kannst deine Funktionen damit https://www.matheretter.de/tools/funktionsplotter/ anschauen.
Leider lässt sich die Skala nicht verändern. Man muss zoomen.

Answer 2

Den kleinsten Funktionswert findest du in dem du die Funktion Ableitest und nach dem Minimum findest, also wenn die Ableitung Null ist. Diesen x-Wert setzt du in f(x) ein und es kommt der Funktionswert raus:

1)f ' (x)=6x+12, f"(x)=0 wenn x=-2 ⇒ Min(f(x))= f(-2)=-37

2)f" (x)= 18x-12, f"(x)=0 wenn x=2/3 ⇒ Min(f(x))= f(2/3)=-9

Comments

@qarim: Gute Lösung. Es ist aber möglich, dass Anonym noch nicht ableiten kann.
@Anonym: Müsst ihr dazu die Scheitelpunktform der Parabel nutzen?

---

ja genau, die Scheitelpunktform hatten wir auf jeden fall schon . Ist das nicht f(x)=a(x-d)^2+e ? Die Ableitung verstehe ich nicht so ganz...

Answer 3

Hat noch jemand hausaufgabe im lambacher schweizer auf wa? :D

Comments

XD auch deswegen hier immer diese GENasiasten...