Schau dir mal die Formel von Georg an.
B ( t ) = B0 * q t
B(t) = neuer Bestand nach t (hier) Jahren
B0 = Anfangsbestand
q = Wachtums bzw. Abnahmefaktor
t = Zeit in (hier) Jahren
Absurdistan
Anfangsbestand 46 Mio = B0
Abnahmefaktor: Die Bevölkerung nimmt jährlich um 2,5 % ab, also
1 - 2,5% = 0,975 oder wie Monty schrieb
100% - 2,5%=97,5%=97,5/100=0,975
Also lautet die Gleichung für die Bevölkerungsentwicklung in Absurdistan
\(B(t)=46\cdot 0,975^t\)
Schlaraffia
Anfangsbestand 20 Mio = B0
Wachstumsfaktor: Die Bevölkerung nimmt jährlich um 6,5 % zu, also
1 + 6,5% = 1,065
Die Gleichung für die Bevölkerungsentwicklung in Schlaraffia lautet dann
\(B(t)=20\cdot 1,065^t\)
Graphisch sieht das so aus:
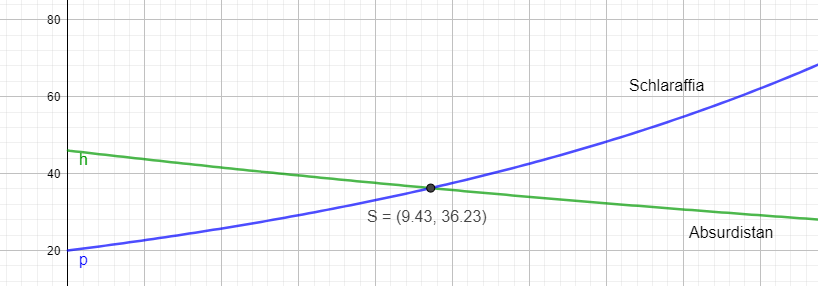 Dort, wo die beiden Graphen sich schneiden, ist die Bevölkerungszahl (ca. 36 Mio) gleich hoch.
Dort, wo die beiden Graphen sich schneiden, ist die Bevölkerungszahl (ca. 36 Mio) gleich hoch.
Schnittpunkte von Graphen berechnest du immer, indem du die Funktionsgleichungen gleichsetzt.
\(46\cdot 0,975^t=20\cdot 1,065^t\)
Die Rechenschritte siehst du in Montys Antwort, wo n = t ist.
Ist es jetzt klarer?
Gruß, Silvia