Funktionsgleichung in Normalform

Question

Aufgabe:

6. Gib die Funktionsgleichung in der Normalform an.
a)  y=(x-2)^2+3
d)  y=(x-5)^2
b)  y=(x+2)^2
e)  y=(x-1)^2-2
c)  y=(x+4)^2-1
f)  y=(x+2)^2-4

Problem/Ansatz:

könnt ihr mir das erklären wie das geht ?

Dankeschön

Answer 1

Hallo,

Lösung durch Ausmultiplizieren

a)  y=(x-2)^2+3

=x^2-4x +4 +3

=x^2-4x +7
d)  y=(x-5)^2

y=x^2-10x +25

usw.

Answer 2

Binomische Formeln zum Ausmultiplizieren benutzen; dann zusammenfassen:

a)y=(x-2)²+3=x²-4x+7
d)  y=(x-5)²=x²-10x+25
b)  y=(x+2)²=x²+4x+4
e)  y=(x-1)²-²=x2-2x-1
c)  y=(x+4)²-1=x²+8x+15
f)  y=(x+2)²-4=x²+4x  

Answer 3

y=(x-2)^2+3    Das ist die Scheitelpunktform der Parabel mit S(2|3).

y=x^2-4x+4+3

y=x^2-4x+7  Das ist die Normalform der Parabel.

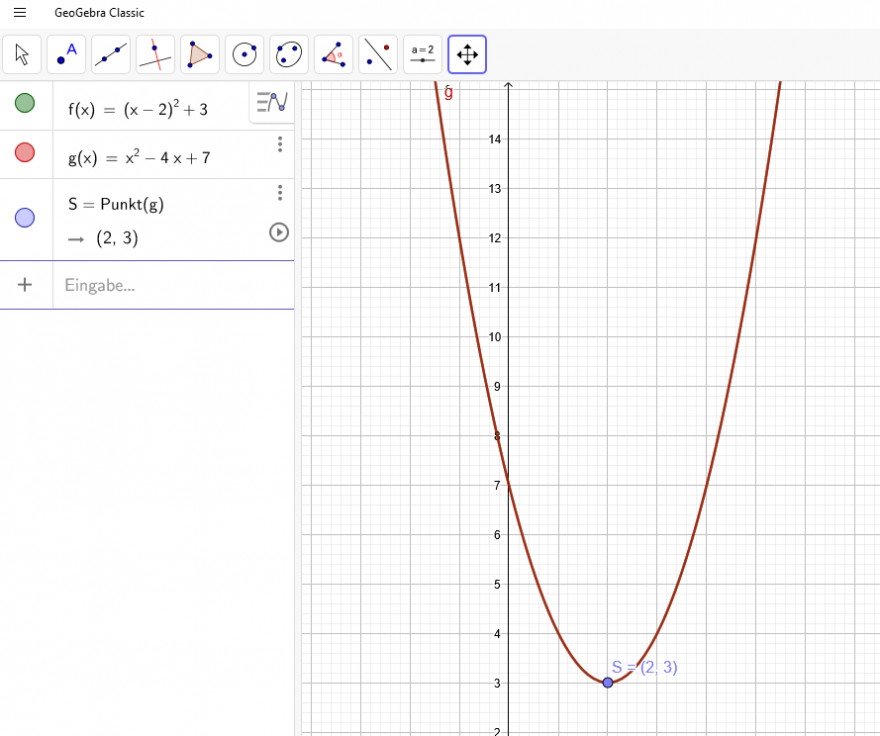
Text erkannt:

\( \equiv \quad \) GeoGebra Classic
As
\( f(x)=(x-2)^{2}+3 \)
\( =\alpha_{0} \)
\( g(x)=x^{2}-4 x+7 \)
\( \mathrm{S}= \) Punkt \( (\mathrm{g}) \)
\( : \)
\( \rightarrow(2,3) \)