Zusammenhang von Ausgangsfunktion und Ableitungsfunktion

Question

Ausgangsfunktion und Ableitungsfunktion

…

Problem/Ansatz:

Skizzieren Sie an den Graphen von f mit f(x)=1/20(-x^4+6x^2+8x+30) die Tangenten in den Punkten P,Q,R und S

Lesen Sie die Steigung der Tangente näherungsweise ab und Überprüfen Sie Ihre Ergebnisse rechnerisch durch einsetzen in die Ableitungsfunktion.

Answer 1

f(x)=\( \frac{1}{20} \)*(-x^4+6x^2+8x+30)

f´(x)=\( \frac{1}{20} \)*(-4x^3+12x+8)

P(-2|...)

f´(-2)=\( \frac{1}{20} \)*[-4*(-2)^3+12*(-2)+8]=\( \frac{4}{5} \)

u.s.w.

Answer 2

Für den Punkt P

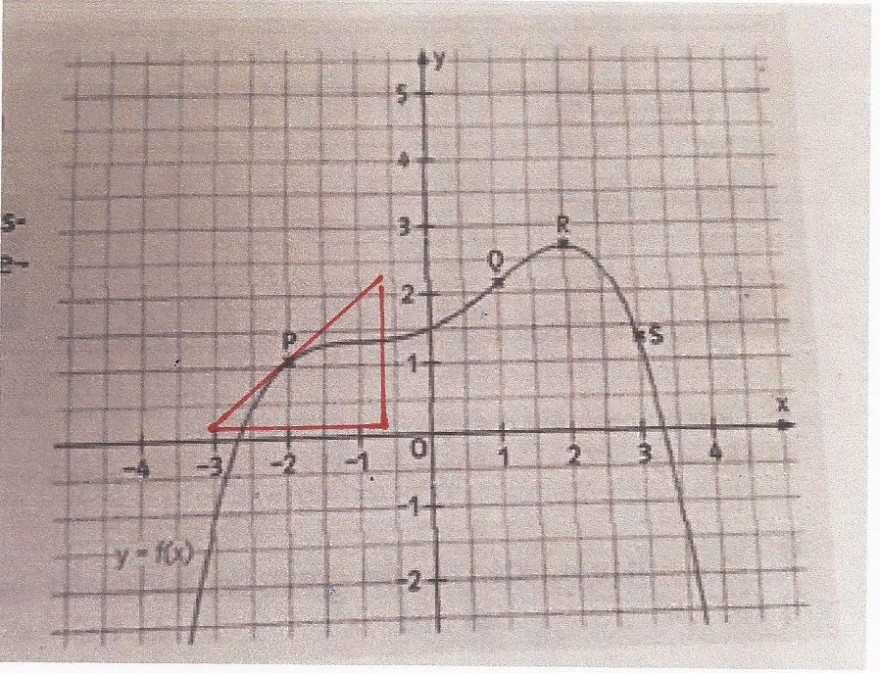Du zeichnest zuächst die Tangente ein
Steigungsdreieck
dann den y-Abschnitt einzeichnen und ausmessen 2.2
dann den x-Abschnitt einzeichnen und ausmessen 2,3

Die Steigung ist 2.2 / 2.3 = 0.96

Dann stelltst du die erste Ableitung auf
f (x) =1/20*(-x^4 + 6*x^2+8*x+30);
f ´( x ) = 1/20 * ( -4x^3 + 12 x + 8 )
Dann einsetzen
x = -2
m = 0.8

Die Übereinstimmung ist nicht so gut.
Jede größer der Maßstab gewählt wird
desto genauer das Ergebnis.