x = -3 wäre im Original eine Nullstelle, Die eine Extremstelle im Intervall (-2, 0) wäre eine Wendestelle und x = 3 …

Question

Eigenschaften einer Stammfunktion erkennen

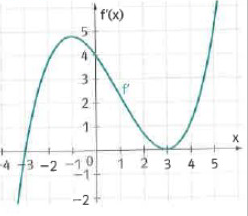
Gegeben ist der Graph der Ableitungsfunktion f´ einer Polynomfunktion f.

Aufgabenstellung:

Kreuze die zutreffende(n) Aussage(n) an!

A ... Die Funktion f hat bei x = -3 eine Nullstelle

B ... Der Graph der Funktion f ist im Intervall (0;3) monoton steigend

C ... An der Stelle -3 hat der Graph von f ein lokales Minimum

D ... An der Stelle 3 hat der Graph von f ein lokales Minimum

E ... Bei x = 3 hat die Funktion f eine Sattelstelle

Bitte um Auskunft!

x = -3 wäre im Original eine Nullstelle, Die eine Extremstelle im Intervall (-2, 0) wäre eine Wendestelle und x = 3 ist sowohl eine Null, als auch eine Extremstelle, nicht wahr?

Comments

wo siehst du bei (-2;0) eine Extremstelle?

Answer 1

Aloha :)

A... kann man nicht sagen

B... ja, die Ableitung ist positiv

C... ja, die erste Ableitung wechselt ihr Vorzeichen von negativ nach positiv

D... nein, die Ableitung ist vor und hinter \(x=3\) positiv.

E... ja, vor und hinter \(x=3\) ist steigt die Funktion, bei \(x=3\) verläuft sie waagerecht.

Comments

Aloha

Puh, danke, habs irgendwie geschafft alle zu treffen. E war mir sofort klar, bei den anderen 2 hatte ich eine Welle (also 50/50)

Muchas gracias amigo, möge die Macht mit dir sein