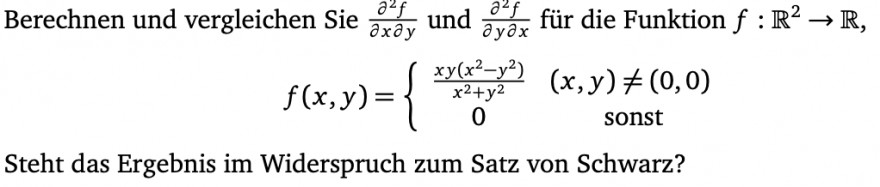
Text erkannt:
Berechnen und vergleichen Sie \( \frac{\partial^{2} f}{\partial x \partial y} \) und \( \frac{\partial^{2} f}{\partial y \partial x} \) für die Funktion \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \)
$$ f(x, y)=\left\{\begin{array}{cc} \frac{x y\left(x^{2}-y^{2}\right)}{x^{2}+y^{2}} & (x, y) \neq(0,0) \\ 0 & \text { sonst } \end{array}\right. $$
Steht das Ergebnis im Widerspruch zum Satz von Schwarz?
Problem/Ansatz:
Wie gehe ich hier genau vor? Könnte jemand einen Lösungsweg zeigen mit dem ich auch analog bei anderen gleichartigen Aufgaben vorgehen kann?