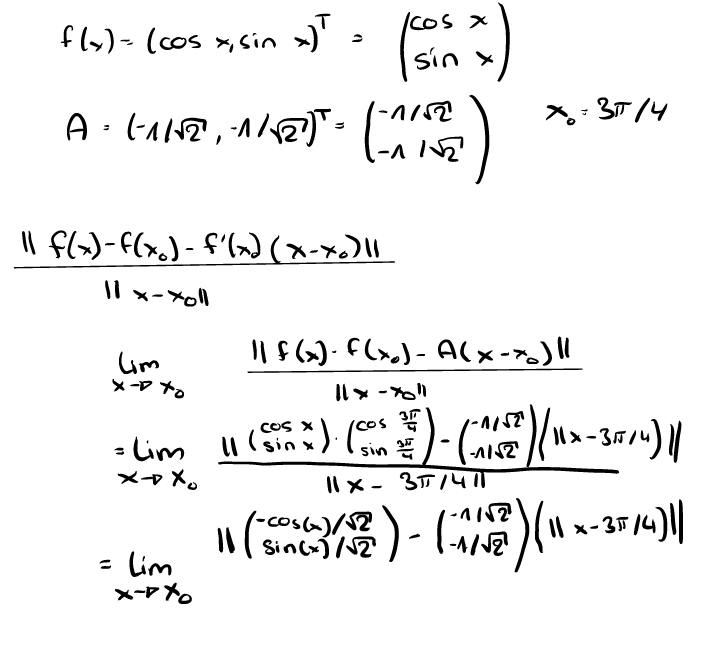Zeige, dass A die Ableitung von f in x_0 ist

Question

Problem/Ansatz:

Text erkannt:

Zeige, dass \( A \) die Ableitung von \( f \) in \( \mathrm{x}_{0} \) (nach Definition \( \left.10.10\right) \) ist.
Bemerke: \( A^{T} \) heißt die transponierte oder gespiegelte Matrix. Beispiele:
$$ (1,2)^{T}=\left(\begin{array}{l} 1 \\ 2 \end{array}\right), \quad\left(\begin{array}{l} 1 \\ 2 \end{array}\right)^{T}=(1,2), \quad\left(\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right)^{T}=\left(\begin{array}{ll} 1 & 3 \\ 2 & 4 \end{array}\right) \text { . } $$
Man benutzt es oft, um ein Vektor in eine einzelne Zeile zu schreiben.
$$ \text { (a) } f: \mathbb{R} \rightarrow \mathbb{R}^{2}, f(x)=(\cos x, \sin x)^{T}, A=(-1 / \sqrt{2},-1 / \sqrt{2})^{T}, \mathrm{x}_{0}=3 \pi / 4 . $$
(b) \( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, f(x, y)=x^{2}-y^{2}, A=(2,-2), \mathrm{x}_{0}=(1,1)^{T} \).
$$ \text { (c) } f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}, f(x, y)=\left(x^{2}+y^{2}, x^{2}-y^{2}\right)^{T}, A=\left(\begin{array}{cc} 4 & -2 \\ 4 & 2 \end{array}\right), \mathbf{x}_{0}=(2,-1)^{T} \text { . } $$

Ich hab die a) versucht zu machen jedoch weiß ich nicht wie ich weiter machen soll oder ob ich überhaupt richtig angegangen bin... Könnte jemand bitte helfen...

Comments

Hallo,

ich würde zunächst prüfen, ob Ihr in der Vorlesung / Lernmitteln.... nicht festgehalten habt, dass die Ableitung einer mehrdimensionalen Funktion in einfacher Weise durch partielle Ableitungen berechnet wird. Stichwort: Jacobi-Matrix, Funktionalmatrix o.ä.

Gruß Mathhilf

---

Ich gucke nochmal nach

---

Text erkannt:

\( f(x)=(\cos x, \sin x)^{\top}=\left(\begin{array}{c}\cos x \\ \sin x\end{array}\right) \)
\( A=(-1 / \sqrt{2},-1 / \sqrt{2})^{\top}=\left(\begin{array}{c}-1 / \sqrt{2} \\ -\wedge 1 \sqrt{2}\end{array}\right) \quad x_{0}=3 \pi / 4 \)
\( f^{\prime}(x)=\left(\begin{array}{cc}-\sin x \\ \cos x\end{array}\right) \)
\( f^{\prime}(3 \pi / 4)=\left(\begin{array}{l}-\frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2}\end{array}\right) \)

Bei a) hat man ja nur f(x), gibt es besondere Regeln beim ableiten weil dieser Weg führt zur nix, da ich nicht das gewünschte A raus bekomme

---

weil dieser Weg führt zur nix

Die Ableitung ist (wenn sie existiert) eindeutig. Es gibt keinen anderen Weg. Also Druckfehler in der Aufgabe? Bevor wir diesem Gedanken näher treten, ein letzter check: Ist wirklich

$$\frac{\sqrt{2}}{2} \neq \frac{1}{\sqrt{2}}?$$

Der allerletzte Check könnte mit einem Taschenrechner erfolgen.

Gruß Mathhilf

---

Oh man .. ja ok

Danke

---

Text erkannt:

c) \( \begin{array}{c}f(x, y)=\left(x^{2}+y^{2}, x^{2}-y^{2}\right)^{\top}=\left(\begin{array}{c}x^{2}+y^{2} \\ x^{2}-y^{2}\end{array}\right) \\ x_{0}=(2,-1)^{\top}=\left(\begin{array}{c}2 \\ -1\end{array}\right) \quad A=\left(\begin{array}{ll}4 & -2 \\ 4 & 2\end{array}\right) \\ \frac{d}{d x} f(x, y)=\left(\begin{array}{ll}2 x \\ 2 x\end{array}\right) \\ \frac{d}{d y} f(x, y)=\left(\begin{array}{cc}2 y \\ -2 y\end{array}\right) & J_{f}(x, y)=\left(\begin{array}{cc}2 x & 2 y \\ 2 x & -2 y\end{array}\right) \\ J_{f} & \end{array} \)

Die b) habe ich jetzt gelöst jedoch bei c) stehe ich auf dem Schlauch. Wie kann ich x_0 was transponiert ist in J_f benutzen? Oder darf ich das einfach so einsetzen?

---

hallo

einfach x=2, y=-1 einsetzen.

lul