berechnen sie das volumen der pyramide

Question

Hallo zsm. Ich habe folgendes Problem gegeben:

In einer quadratischen Pyramide verhält sich die Grundkante zur Körperhöhe wie a : h = 5 : 6. Die Oberfläche beträgt = 1440cm2. berechnen sie das volumen der pyramide

ich habe versucht das ganze durch umformen zu berechnen. zuerst die brüche multipliziert = a= 5/6 x h und dann für a in die oberflächen formel eingesetzt.

die lösung ist 3200 ich hate 11450

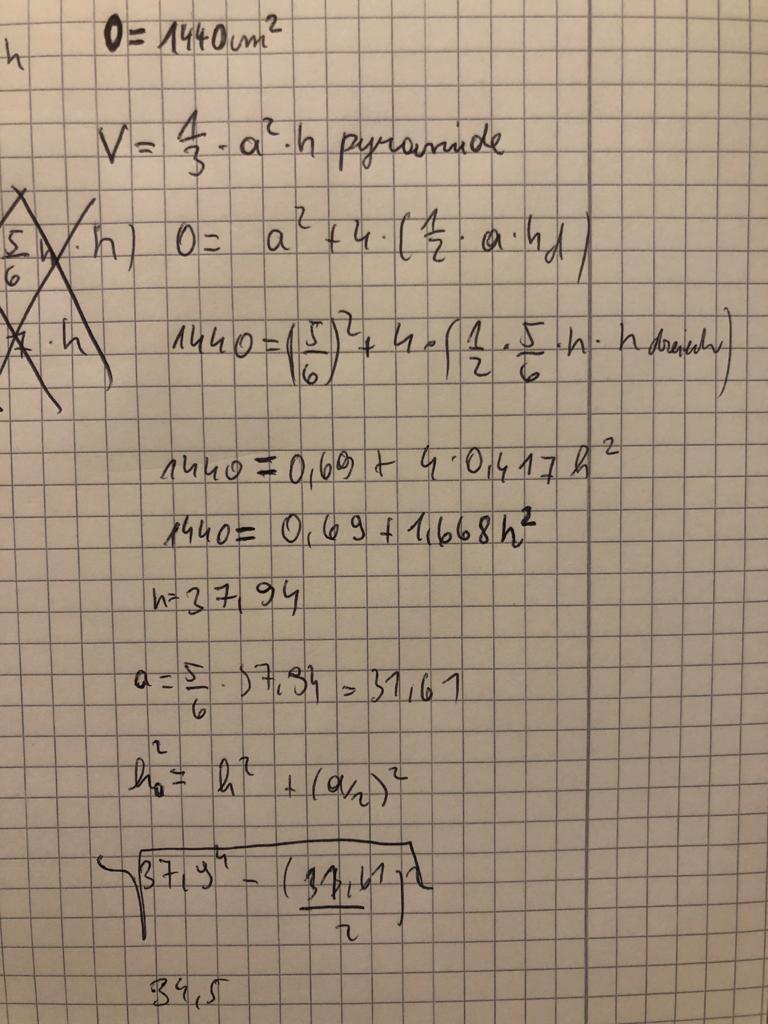
Text erkannt:

$0=1440 \mathrm{~cm}^{2}$
$V=\frac{1}{3} \cdot a^{2} \cdot h$ pyrounude
51
4) $1440=\left(\frac{5}{6}\right)^{2}+4 \cdot\left(\frac{1}{2} \cdot \frac{5}{6} \cdot h \cdot\right.$ hound $)$
$1440=0,69+4 \cdot 0,417 h^{2}$
$1440=0,69+1,668 h^{2}$
$h=37,94$
$\left.a=\frac{5}{6} \cdot 57,3\right\}=31,61$
$h_{0}^{2}=h^{2}+(a / 2)^{2}$
$\sqrt{ \left.37, y^{4}-\frac{(34,4)}{2}\right)^{2}}{34,5}$

Answer 1

Die Höhe k einer Seitenfläche ist k=$\sqrt{(a/2)^2+h^2}$.

Comments

Vielen Dank!

Answer 2

Du hast für den Term 4*0,471 h² wohl h und h_Dreieck identifiziert.

Das stimmt nicht, denn h und h_Dreieck und a/2 bilden ein rechtwinkliges

Dreieck mit den Katheten h und a/2 , also

h² + (a/2)² =  h_Dreieck²  also   h_Dreieck = Wurzel(61/36) * h.

Comments

Vielen Dank!

Answer 3

"In einer quadratischen Pyramide verhält sich die Grundkante zur Körperhöhe wie a : h = 5 : 6. Die Oberfläche beträgt = 1440cm². Berechnen sie das Volumen der Pyramide."

Text erkannt:

1.) $0=a^{2}+2 \cdot a \cdot h_{a}$
2. $) V=\frac{1}{3} a^{2} \cdot h$
$h_{a}^{2}=\left(\frac{a}{2}\right)^{2}+h^{2} \rightarrow \rightarrow h_{a}=\sqrt{\frac{a^{2}}{4}+h^{2}}$
1. $O=a^{2}+2 \cdot a \cdot \sqrt{\frac{a^{2}}{4}+h^{2}}$
$\frac{a}{h}=\frac{5}{6} \rightarrow \rightarrow a=\frac{5}{6} \cdot h$
1. $0=\left(\frac{5}{6} \cdot h\right)^{2}+2 \cdot \frac{5}{6} \cdot h \cdot \sqrt{\frac{\left(\frac{5}{6} \cdot h\right)^{2}}{4}+h^{2}}$
1. $0=\frac{25}{36} h^{2}+\frac{5}{3} \cdot h \cdot \sqrt{\frac{169}{144} h^{2}}$
1.) $O=\frac{25}{36} h^{2}+\frac{5}{3} \cdot h \cdot \frac{13}{12} \cdot h=\frac{5}{2} \cdot h^{2} \rightarrow \rightarrow 1440=\frac{5}{2} \cdot h^{2} \rightarrow \rightarrow h^{2}=576 \rightarrow \rightarrow h=24 \rightarrow \rightarrow h^{3}=13824$
2. $) V=\frac{1}{3} \cdot\left(\frac{5}{6} \cdot h\right)^{2} \cdot h=\frac{25}{108} h^{3} \rightarrow \rightarrow V=\frac{25}{108} \cdot 13824=3200$

Comments

vielen dank! besser kann man es nicht erklären