Stelle die Gleichung der Geraden von g und h.

Question

Aufgabe:

Stelle die Gleichung der Geraden g(A,B) und h(C,D) auf. Ermittle die gegenseitige Lage der Geraden g und h und berechne wenn möglich, den Schnittpunkt und den Schnittwinkel.

A(3/2), B(5/3), C(-4/0), D(2/3)

Answer 1

Hallo,

g(A,B) ,   A(3/2), B(5/3)             g(x) = mx+b

Steigung   m = \( \frac{3-2}{5-3} \)     m=  1/2

g(x) = 1/2 x+b     einen Punkt einsetzen

A ( 3| 2)        2= 1/2 *3 +b       b = 4/3  

g(x)  = 1/2 x +4/3

auf die Art und Weise die zweite Gerade auch bestimmen, dann g(x) = h(x)  setzen um einen möglichen Schnittpunkt zu bestimmen ...

Answer 2

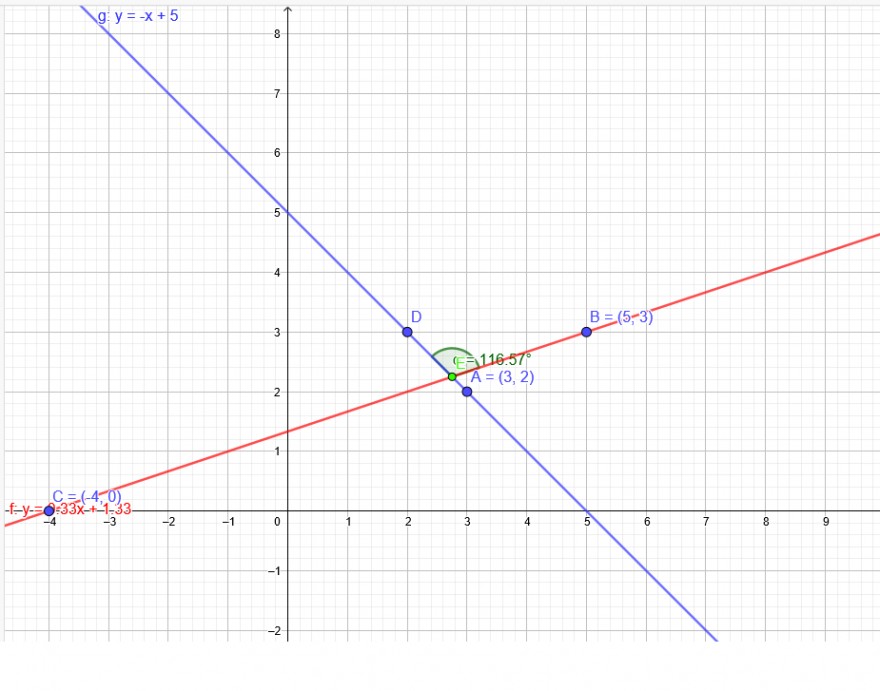
Falls du mal Geraden hast, die sich schneiden: f(B,C) und g(A,D)

Dann findest du f(x) =\( \frac{1}{3} \) x+\( \frac{4}{3} \)       g(x)=-x+5

f(x)= g(x)   ergibt dann den Schnittpunkt E(2,75|2,25)

Zur Berechnung des Schnittwinkels existiert nun die Formel:

tanα=|\( \frac{m₂-m₁}{1+m₁*m₂} \)|

g(x)=-1*x+5    hat die Steigung  m₂=-1

f(x)=\( \frac{1}{3} \) x+\( \frac{4}{3} \)      hat die Steigung m₁=\( \frac{1}{3} \)    

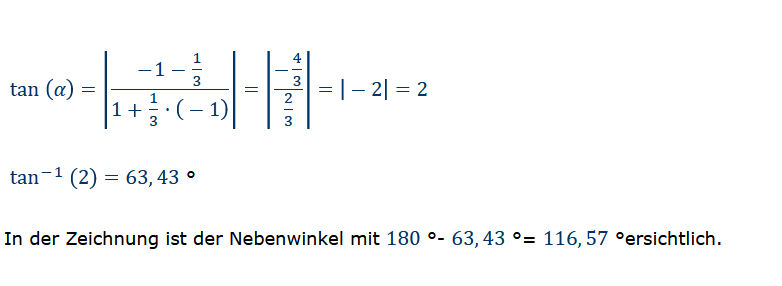
Text erkannt:

$$ \tan (\alpha)=\left|\frac{-1-\frac{1}{3}}{1+\frac{1}{3} \cdot(-1)}\right|=\left|\frac{-\frac{4}{3}}{\frac{2}{3}}\right|=|-2|=2 $$
\( \tan ^{-1}(2)=63,43^{\circ} \)
In der Zeichnung ist der Nebenwinkel mit \( 180^{\circ}-63,43^{\circ}=116,57^{\circ} \) ersichtlich.