Gleichung einer Geraden h, die Gerade g orthogonal schneidet.

Question

Aufgabe:

Geben Sie eine Gleichung der Geraden h an, die die Gerade g orthogonal schneidet.

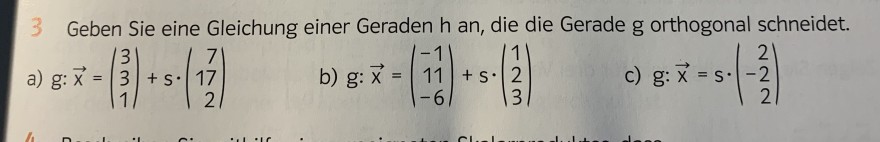
Text erkannt:

3 Geben Sie eine Gleichung einer Geraden \( \mathrm{h} \) an, die die Gerade g orthogonal schneidet.
a) g: \( \vec{x}=\left(\begin{array}{l}3 \\ 3 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{r}7 \\ 17 \\ 2\end{array}\right) \)
b) \( g: \vec{x}=\left(\begin{array}{r}-1 \\ 11 \\ -6\end{array}\right)+s \cdot\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right) \)
c) g: \( \vec{x}=s \cdot\left(\begin{array}{r}2 \\ -2 \\ 2\end{array}\right) \)

(ich habe die Vektoren fotografiert, weil ich das sonst hier nicht übernehmen könnte)

Problem/Ansatz:

Ich komme hier nicht weiter und weiß nicht wie ich die Aufgabe lösen kann. Ich sie aber gerne verstehen wollen. Könnte mir das daher vielleicht jemand exemplarisch an einer der Aufgaben erklären, damit ich es nachvollziehen kann?

Answer 1

Benutze den gleichen Stützvektor als Ortsvektor des Schnittpunktes und einen Vektor der mit dem Richtungsvektor der Geraden das Skalarprodukt 0 ergibt.

$$a) ~ h: ~\vec x = \begin{pmatrix} 3\\3\\1 \end{pmatrix} + r \cdot \begin{pmatrix} 17\\-7\\0 \end{pmatrix} \newline b) ~ h: ~\vec x = \begin{pmatrix} -1\\11\\-6 \end{pmatrix} + r \cdot \begin{pmatrix} 1\\1\\-1 \end{pmatrix} \newline c) ~ h: ~\vec x = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + r \cdot \begin{pmatrix} 1\\2\\1 \end{pmatrix}$$

Answer 2

Der bestimmt Artikel trifft in der vom FS formulierten Aufgabenstellung nicht zu. Es gibt unendlich viel geforderte Geraden. Sie liegen in einer beliebigen Ebene, auf der der Richtungsvektor der Geraden senkrecht steht. In Aufgabe a) ist ein Beispiel:

 \( \vec{x}=\left(\begin{array}{l}3 \\ 3 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{r}2 \\ -1 \\ 1,5\end{array}\right) \) Weil das Skalarprodukt \( \begin{pmatrix} 2\\-1\\1,5 \end{pmatrix} \) ·\( \begin{pmatrix} 7\\17\\2 \end{pmatrix} \)  =0 ist.