Warum sind die Winkel gleichgroß? Beweis

Question

ich stehe vor folgendem Problem:

Im Dreieck \( A B C \) seien \( H \) der Höhenschnittpunkt und \( O \) der Mittelpunkt des Umkreises. Dann sind die Winkel \( \angle H A B \) und \( \angle O A C \) gleich groß

Dafür haben wir folgende Lösung bekommen:

Wir haben zwei Fälle zu unterscheiden:

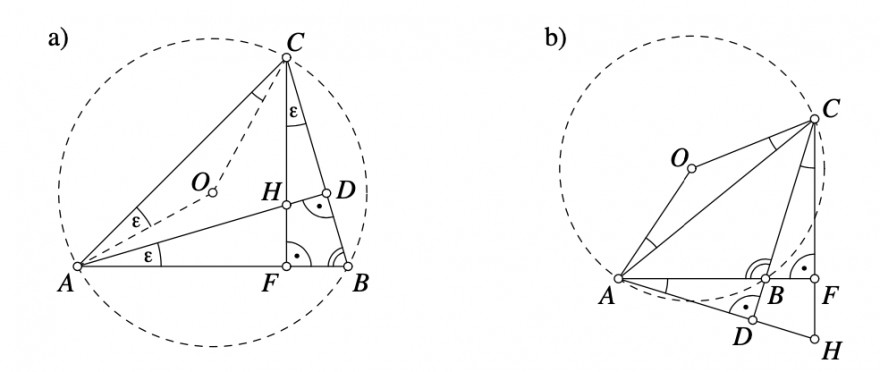
a) Das Dreieck ABC ist spitzwinklig

b) Das Dreieck ABC hat einen stumpfen Innenwinkel, sodass der Höhenschnittpunkt H außerhalb des Dreiecks liegt.

Bezeichnen wir \( \angle H A B=\angle D A B \equiv \varepsilon \) , so können wir im ersten Fall wie folgt schließen:

\( \triangle B D A \) ist rechtwinklig, also ist \( \angle A B D=\angle A B C=90^{\circ}-\varepsilon \). Letzterer ist Peripheriewinkel über der Sehne AC des Umkreises, somit ist der zugehörige Zentriwinkel doppelt so groß: \( \angle A O C=2 \angle A B C=180^{\circ}-2 \varepsilon . \) Da \( \triangle A O C \) gleichschenklig ist, sind die Basiswinkel dieses Dreiecks nach dem Innenwinkelsatz \( \angle O A C=\angle O C A=\frac{1}{2}\left[180^{\circ}-\left(180^{\circ}-2 \varepsilon\right)\right]=\varepsilon \).

Im Falle eines stumpfwinkligen Dreiecks sei \( \angle H A B=\angle D A B=\varepsilon \). Der Außenwinkel ABC des rechtwinkligen Dreiecks BDA beträgt somit \( 90^{\circ}+\varepsilon \) und ist gleichzeitig Peripheriewinkel von AC, der nicht auf derselben Seite wie der Zentriwinkel AOC liegt. Daher ist \( \angle A O C=360^{\circ}-2 \angle A B C=180^{\circ}-2 \varepsilon \).

Wie in a) ist \( \triangle A O C \) gleichschenklig, damit gilt \( \angle O A C=\varepsilon=\angle H A B \)

Text erkannt:

b)

Leider verstehe ich wirklich fast nur Bahnhof.. ich habe mir schon einige Videos zu Peripheriewinkel und Zentriwinkel angeschaut, aber die Lösung kann ich trotzdem nicht nachvollziehen.

Kann mir das bitte jemand für Laien erklären? Vielleicht einfach nochmal in eigenen Worten wiedergeben damit ich es besser verstehe? Dadrüber wäre ich wirklich sehr dankbar!

Answer 1

Hallo,

Die Basics:

Den gelben Winkel nennt man Peripherie- oder Umfangswinkel. Umfangswinkel weil sich der Scheitel \(B\) des Winkels auf dem Umfang (des Kreises) befindet. Der rote Winkel ist der Mittelpunktswinkel. Mittelpunktswinkel weil der Scheitel identisch zum Mittelpunkt \(O\) (des Kreises) ist. Es gilt immer: $$\angle COA = 2 \beta$$der Mittelpunktswinkel ist stets doppelt so groß wie der Peripheriewinkel.

Die Übersicht:

Das Dreieck \(\triangle AOC\) ist gleichschenklig, da die Schenkel \(|AO|\) und \(|OC|\) gleich lang sind (Radius). Also ist das Dreieck auch symmetrisch zur Achse durch \(OM_b\). Der Punkt \(M_b\) ist der Mittelpunkt der Dreiecksseite \(b=AC\). Also muss der Winkel \(\angle M_bOA = \frac 12 \angle COA = \beta\) sein (gelb).

Die Dreiecke \(\triangle AOM_b\) und \(\triangle ABD\) sind beide rechtwinklig und habe beide einen gemeinsamen Winkel \(\beta\). Man sagt die Dreiecke sind ähnlich. Also muss der dritte Winkel \(\angle BAD= \varepsilon\) (blau) bzw. \(\angle OAM_b\) (blau) auch gleich sein.

Zum Detail des Beweises:

△BDA ist rechtwinklig, also ist \( \angle A B D=\angle A B C=90^{\circ}-\varepsilon \).

Mit \(\angle ABC\) ist \(\beta\) gemeint. Korrekt wäre aber \(\beta = \angle CBA\). △BDA ist rechtwinklig (schwarzer Winkel bei \(D\)), weil die Höhe immer im rechten Winkel auf der zugehörigen Grundseite steht. \(\angle DBA = \beta\) (gelb) und \(\varepsilon = \angle BAD\) (blau bei \(A\))

Letzterer (\(\beta\)) ist Peripheriewinkel über der Sehne AC des Umkreises, somit ist der zugehörige Zentriwinkel doppelt so groß: \( \angle COA =2 \angle A B C=180^{\circ}-2 \varepsilon . \) 

Siehe Bild ganz oben. Mit \(\angle ABC\) ist \(\beta\) (gelb) gemeint. \(\beta + \varepsilon = 90°\) wegn der Winkelsumme im Dreieck \(\triangle ABD\). Also ist der Mittelpunktswinkel$$\angle COA = 2 \beta = 2(90°-\varepsilon) = 180° - 2\varepsilon$$

Da \( \triangle A O C \) gleichschenklig ist, sind die Basiswinkel dieses Dreiecks nach dem Innenwinkelsatz \( \angle O A C=\angle O C A=\frac{1}{2}\left[180^{\circ}-\left(180^{\circ}-2 \varepsilon\right)\right]=\varepsilon \).

Statt \(\angle OCA\) muss es \(\angle ACO\) heißen. \(\angle ACO\) und \(\angle OAC\) sind die blauen Basiswinkel im gleichschenkligen Dreieck \(\triangle AOC\). Hier wird die Dreieckssumme in diesem Dreieck betrachtet.$$\begin{aligned} \underbrace{\angle COA}_{=\text{Mittelpunksw.}} + \underbrace{\angle OAC + \angle ACO}_{=\text{Basisw.}}  &= 180° &&|\, \angle ACO = \angle OAC \\ \angle COA + 2\angle OAC &= 180° &&|\, - \angle COA \\ 2\angle OAC &= 180° - \angle COA &&|\, \div 2 \\ \angle OAC &= \frac 12\left( 180° - \angle COA \right) &&|\, \angle COA = 180° - 2\varepsilon \\  \angle OAC &= \frac 12\left( 180° - (180° - 2\varepsilon)\right) \\ \angle OAC &= \frac 12\left( 180° -180° + 2\varepsilon \right) \\ \angle OAC&= \frac 12 \cdot 2 \varepsilon \\ \angle OAC&= \varepsilon\end{aligned}$$Falss Du noch Fragen hast, so melde Dich bitte.

Gruß Werner