a) Geben Sie zunăchst die Parameter n und p für diese Wahrscheinlichkeitsverteilung an.
n = 10 ; p = 1/3
b) Ermitteln Sie die Wahrscheinlichkeit für jedes k mit einer Genauigkeit von vier Stellen nach dem Komma!
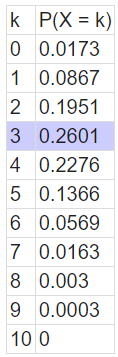
c) Erstellen Sie ein Histogramm!
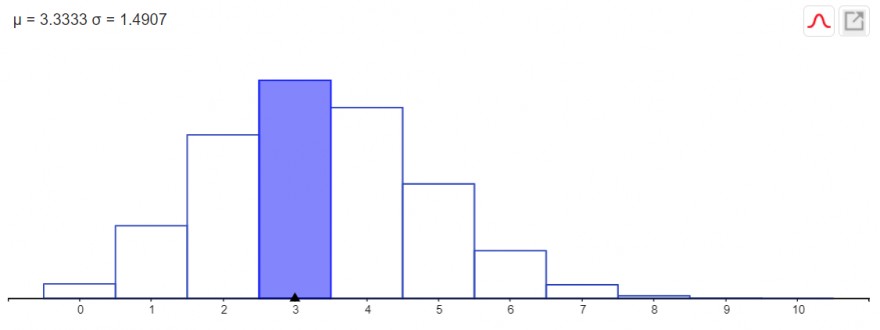
d) Geben Sie eine Gleichung an, mit der die Wahrscheinlichkeit berechnet werden kann, dass Mike den Test zu besteht, wenn dafür mindestens acht richtige Antworten erforderlich sind? Ermitteln Sie diese Wahrscheinlichkeit!
P(X ≥ 8) = ...