: Warum kriege ich die falsche Höhe raus? Flächeninhalt mit Vektoren und Ebene berechnen

Question

Aufgabe:

Die Aufgabe lautet:

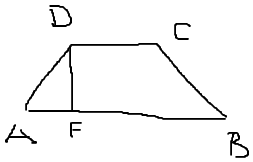
Die Punkte A (1/1/2), B (3/5/-2), C (2/3/2) und D (-4/-9/14) sind die Ecken eines Trapezes. Berechnen Sie seinen Flächeninhalt.

Problem/Ansatz:

Diese Aufgabe wurde schon im Forum behandelt, dennoch muss ich sie auf einem anderen Rechenweg bearbeiten als die hier im Forum geklärte Aufgabe.

a+c/2*h, dass ist die Formel fürs Trapez.

Wie man auf A und C kommt ist mir klar.

Die Angaben sind 6cm und 8cm für die Seitenlängen a und c.

Dann habe ich die Normalform der Ebene: x - (-4,-9,14)*(2,4,-4) gebildet.

Daraus habe ich dann die Koordinatenform 2x+4y-4z=-100 gebildet.

Zudem die Gerade AB: (1,1,2)+s(2,4,-4).

Die Gerade AB in die Koordinatenform der Ebene eingesetzt und s= -2,7 rausbekommen.

-2,7 in Gerade AB eingesetzt, das Ergebnis subtrahiert von Punkt D um Vektor FD zubekommen.

FD Koordinaten hoch zwei in Wurzel genommen und 26,8 rausbekommen. Zuvor bei FD die Koordinaten (-0,4,-0,8,26,8) errechnet.

Ich weiß es gibt viele Möglichkeiten es zulösen, ich soll es aber genau nach diese Methode machen. Sprich Ebene mit Punkt D bilden und mit der Gerade AB gleichsetzten, Durchstoßpunkt finden, den Vektor FD bilden und alle Werte Quadrieren in der Wurzel. Dann Flächeninhaltsformel anwenden.

Kleine Hilfe was ich meine:

Answer 1

und s= -2,7 rausbekommen.

Korrekt ist s = -49/18.

Zuvor bei FD die Koordinaten (-0,4,-0,8,26,8) errechnet.

-0,4 und -0,8 sind falsch wegen falschem s. Die 26,8 sind mir unerklärlich.

Comments

Woher ist die -49 und die 18?

Meine Rechnung:

2*(-4)+4*(-9)-4*14=-100
2x+4y-4z=-100

2(1+2s)+4(1+4s)-4(2-4s)=-100
36s-2=-100                                           +2 & /36
s=-2,72

---

Wie bist du denn auf den Normalenvektor gekommen? Ich erhalte (24|-12|0) bzw. (2|-1|0) als Kreuzprodukt der Richtungsvektoren DA und DC.

---

Als Normalvektor nehme ich ganz einfach den Richtungsvektor von AB.

Ich baue ja eine Ebene auf, zuerst in der Normalenform, dann in der Koordinatenform.

Normalform der Ebene: x - (-4,-9,14)*(2,4,-4)

Koordinatenform 2x+4y-4z=-100

Mit Punkt D, der auf der Ebene liegt bilde ich die Koordinatenform. Dann setzte ich mit der Gerade AB gleich um den Lotfußpunkt/Durchstoßunkt zu errechnen. Dann Länge FD errechnen und ich habe die Trapezhöhe.

Warum kommt beim Gleichsetzen von Gerade und Ebene  s = -2,7 raus, was offensichtlich falsch ist?

---

Als Normalvektor nehme ich ganz einfach den Richtungsvektor von AB

Ein Normalenvektor steht senkrecht auf einer Ebene und liegt nicht darin.

---

Er liegt ja senkrecht drauf. Das Trapez ist demnach "senkrecht" und die Ebne waagerecht.

Guck dir das Beispiel von einer anderen Aufgabe aus meinem Buch an. Habe es auf Google Drive hochgeladen, da es ja hier nicht erlaubt ist. Dort wird auch der Richtungsvektor CB als Normalvektor benutzt.

Link zum Beispiel:

https://drive.google.com/file/d/16u1hYSUZXAF5vTNhF9bYKEU6TkR5HwY5/view?usp=sharing

---

Das Trapez liegt doch auf einer Ebene. Also müssen auch alle vier Punkte auf dieser Ebene liegen.

---

Habe den Link hinzugefügt vom Beispiel.

---

s=-2,72

Das sieht schon etwas besser aus.

Aber eigentlich kommen da noch unendlich viele Zweier. Wenn du die abschneidest (a.k.a. rundest), dann darfst du dich nicht wundern, dass das Ergebnis falsch ist.

Rechne stattdessen mit Brüchen. Mit denen bekommst du

        \(s = -\frac{49}{18}\).

Answer 2

Mir war nicht klar, dass du mit einer Hilfesebenen arbeitest.

Wenn du die Koordinaten in die Gleichung der Hilfsebene einsetzt, erhältst du

\(2\cdot(1+2x)+4\cdot (1+4s)-4\cdot (2-4s)=-100\\ 2+4s+4+16s-8+16s=-100\\ -2+36s=-100\\ 36s=-98\\ s=-\frac{98}{36}=-\frac{49}{18}\)