Logarithmen berechnen und Gleichungen

Question

Aufgabe:

Die Bevölkerung eines Landes wächst jähr-
lich um 1,4%. Der Anfangsbestand beträgt
20 Millionen.

a) Begründen Sie, dass die Bevölkerungs-
zahl durch die Exponentialfunktion
N(t) = 20 - 1,014' erfasst wird.
(t: Jahre, N: Millionen)
b) Nach welcher Zeit werden 30 Millionen
Einwohner erreicht?

Problem/Ansatz

Weiß nicht wie ich das rechnen soll ♀️

Answer 1

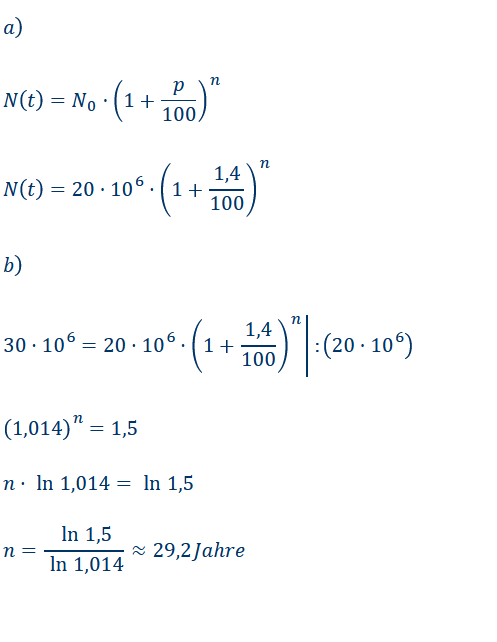
Text erkannt:

a)
\( N(t)=N_{0} \cdot\left(1+\frac{p}{100}\right)^{n} \)
\( N(t)=20 \cdot 10^{6} \cdot\left(1+\frac{1,4}{100}\right)^{n} \)
b)
\( 30 \cdot 10^{6}=20 \cdot 10^{6} \cdot\left(1+\frac{1,4}{100}\right)^{n} \mid:\left(20 \cdot 10^{6}\right) \)
\( (1,014)^{n}=1,5 \)
\( n \cdot \ln 1,014=\ln 1,5 \)
\( n=\frac{\ln 1,5}{\ln 1,014} \approx 29,2 \) Jahre

Comments

Ich will nicht zu pingelig sein aber es
muß anstelle
n(t) = n0 * ( 1 + p/100 ) ^n
heißen
n(t) = n0 * ( 1 + p/100 ) ^t

mfg Georg

---

Ja, danke sehr, ich hatte die Ausgangsformel K_n=K_0*(1+\( \frac{p}{100} \))^n zu sehr verinnerlicht.