Aufgabe: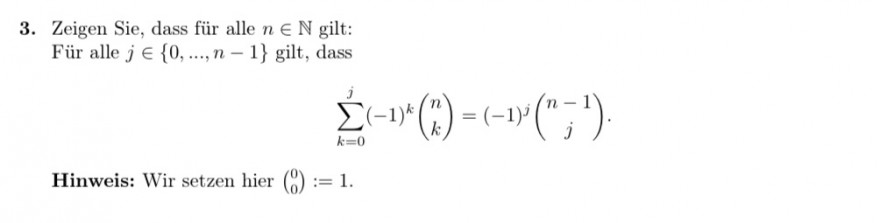
Text erkannt:
3. Zeigen Sie, dass für alle \( n \in \mathbb{N} \) gilt:
Für alle \( j \in\{0, \ldots, n-1\} \) gilt, dass
$$ \sum \limits_{k=0}^{j}(-1)^{k}\left(\begin{array}{l} n \\ k \end{array}\right)=(-1)^{j}\left(\begin{array}{c} n-1 \\ j \end{array}\right) . $$
Hinweis: Wir setzen hier \( \left(\begin{array}{l}0 \\ 0\end{array}\right):=1 \).