Wie kann die Laufzeit für n abgeschätzt werden, die sich nicht als 2k−1 darstellen lassen?

Question

Aufgabe:

Sei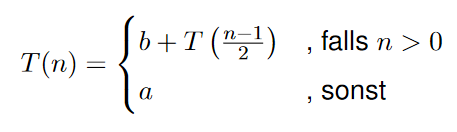

a) Beweisen Sie mittels vollständiger Induktion, dass die geschlossene Form gilt. BedenkenSie, dass wir vereinfachend annehmen, dass n= 2k−1 ist und daher die Induktion auch über k vollzogen werden kann.

b) Wie kann die Laufzeit für n abgeschätzt werden, die sich nicht als 2k−1 darstellen lassen?

Text erkannt:

\( T(n)=\left\{\begin{array}{ll}b+T\left(\frac{n-1}{2}\right) & , \text { falls } n>0 \\ a & , \text { sonst }\end{array}\right. \)

Problem/Ansatz:

Hinweis: Die Kostenfunktion ist monoton.