f(x) = x^2 + ln(x)
Definitionsbereich ist x > 0
f'(x) = 2·x + 1/x > 0
2·x + 1/x > 0 Damit ist die Funktion streng monoton steigend.
f''(x) = 2 - 1/x^2 = 0
x = √2/2 = 0.7071067811
f(√2/2) = (√2/2)^2 + ln(√2/2) = 0.1534264097
f''(x) > 0 Linkskrümmung, Konvex für x > √2/2
f''(x) < 0 Rechtskrümmung, Konkav für x < √2/2
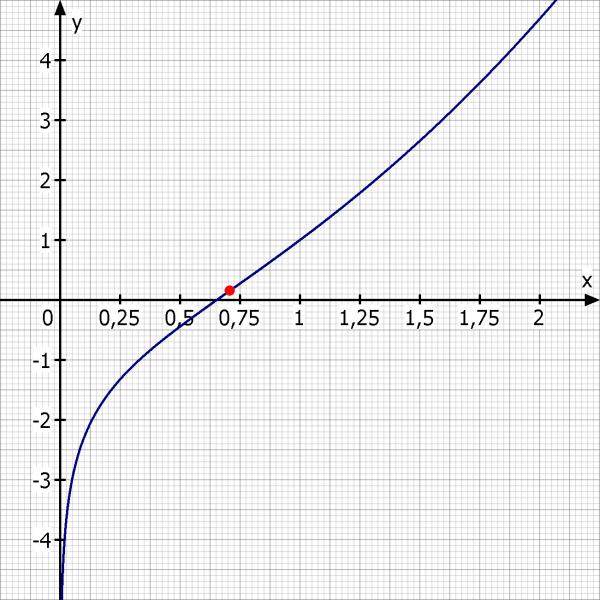
Skizze